He was hoping to publish with a mood of "Russia - in the semi-finals," but was not enough. Although for me the character was always higher than the result, and the character I saw. Thanks guys. We continue to improve in that we can. They are in football, we are in the design of printed circuit boards. Let's go, the sixth part. It examines the effect of losses in the line on the duration of the signal front, gives a model of crosstalk and provides recommendations for reducing them.
In the
previous article it was shown that line inconsistency leads to the appearance of reflections and signal distortion. All matching methods involve ensuring equal load impedances and / or source impedance of the signal line. It follows that if the load impedance is variable and depends on a certain parameter, it is impossible to ensure exact matching. For example, an input cascade of logical elements is always characterized by an equivalent input capacity (usually these are picofarad units). The voltage at the input capacitor V during transients, and hence its impedance
depend on time. The reflections arising in this case are expressed in slowing the front duration by a time τ ≈ 2.2 ∙ Z
0 C (by analogy with an RC circuit). If the length of the front of the source t
R is small compared to τ, then the process of charging the capacitor will determine the duration of the front at the far end of the line.
In a real signal line, the signal front slows down not only with an increase in the capacitive load on it, but also because of losses, which are caused by ohmic losses and leakages in the dielectric. In fig. 1 shows a lossy line model, where the series resistance
models ohmic losses (including skin effect), and resistance
dielectric (here tg (δ) is the loss tangent, a characteristic of the dielectric material). The increase in losses with increasing frequency leads to the fact that the high-frequency components of the signal are attenuated more significantly, which leads to a slowing of the signal front. Eric Bogatin in [1] gives a formula for estimating the front duration at the output of a signal line with losses of length L and a dielectric with permeability ε and loss tangent tg (δ):
Further, from the condition ∆t
R = t
R OUT -t
R IN <0.1 ∙ t
R IN, we can derive an estimator of the need to take into account the effects associated with losses in the signal line.
R.1.
For a signal line, the length L of which meets the criterion L [cm] <5 / (tg (δ) √ε) ∙ t R [ns], the effect of losses on the duration of the signal front can be ignored. For the FR4 dielectric, this condition takes the form L [cm] <125 ∙ t R [ns].
As can be seen from this recommendation, in most applications, in the design of printed circuit boards, you can use a lossless signal line model, where R
LEAK = ∞ and R
SER = 0.
Another source of losses is cross coupling with adjacent conductors (eng. Coupling), which leads to distortions of the signal in the active line (due to losses in the near field) and to induced crosstalk (eng. Crosstalk) in the passive line. The effect arises due to two physical principles - electrical (capacitive) coupling and magnetic (inductive) coupling. In fig. 2 shows the defining parameters of the cross connection - the mutual inductance L
M and the mutual capacitance C
M , depending primarily on the geometry and parameters of materials.
Shown in fig. 3 equivalent cross-connection circuitry can be used when performing calculations and simulations. Moreover, the number N of such consecutive links must be the larger, the higher the electrical length of the TD lines and the required spectral band of the BW model:
Capacity C
L and inductance L
L of the links can be calculated by the formulas:
The main difficulty in simulating an equivalent cross-coupling scheme is in calculating the values of L
M and C
M per link. For some cases, there are evaluative analytical relations [2]; in general, specialized software based on numerical methods is used to solve this problem.
R.2.
The mutual inductance and mutual capacitance values decrease with increasing distance between the conductors and with decreasing distance between the conductor and the supporting layer. In addition, the presence of cuts in the support layer leads to a significant increase in mutual inductance.
Electrical and magnetic coupling leads to energy loss and signal distortion in the active line and the appearance of a signal in the passive line. The currents of capacitive I
C and inductive I
M coupling (Fig. 4) are unidirectional towards the source (near-end) and oppositely directed towards the load (far-end):
The equivalent circuit is electrically short (for the time delay of which TD <1/5 ∙ t
R of the passive line is performed, shown in Fig. 5, where the sources of electrical energy are defined by the formulas:
The scheme is simplified and applicable only to estimate the amplitude of crosstalk. However, for this scheme, analytical relations are derived, which show the main dependencies that are also performed for more complex cases:
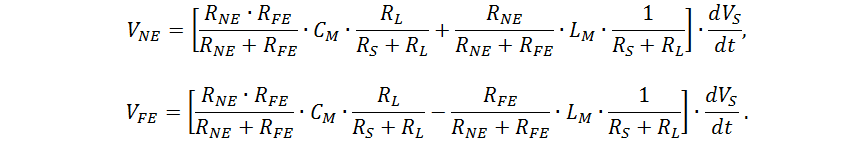
R.3.
Methods to reduce crosstalk:
- Increasing the duration of the signal fronts in the active line (English aggressor, active line).
- Reducing the parallel section of lines.
- Increase the distance between the conductors. There are recommendations for the minimum distance between the edges of printed tracks s ~ 6 6 h or s ~ 3 ∙ w, where h is the distance to the reference layer, w is the width of the track.
- Reducing the distance between the conductor and the support layer.
- Selection of resistances at the ends of the active and passive (English victim, quiet line) lines.
- The use of shielding conductors (English guard trace), shorted to the support layer at the ends and, if possible, along the length (about three vias for the length t R ∙ v).
- The use of embedded microstrip (eng. Embedded microstrip) or strip lines, for which, due to dielectric symmetry, V FE ≈ 0 is performed.
In fig. 6 shows oscillograms for measuring crosstalk between two 50-ohm microstrip lines on the experimental board in two cases: w ~ 2.5 mm, s ~ 0.6 mm, h = 1.39 mm and w ~ 0.6 mm, s ~ 1.9 mm, h = 0.3 mm. The length of the parallel sections of the tracks is about 30 cm. It is worth paying attention to the fact that the duration of the fronts of the signal on the active line significantly exceeds typical values for high-speed digital printed circuit boards. The magnitude of the noise in Fig. 5 should not be considered as characteristic, these oscillograms are primarily a visual representation of the effect on the magnitude of the interference signal duration, the distance between the conductors and the proximity of the support layer.

The above theory for simplicity considered an example of two conductors. However, it is important to understand that for digital printed circuit boards, a typical situation is when several signal lines synchronously change their state. Since crosstalk from several active lines are added, then the amount of interference can become critical, leading to incorrect system operation. In this case, specialized software is used for numerical simulation, but the fundamental principles for reducing the amount of cross-talk remain the same as the above recommendation.
Literature.
[1] Bogatin E. "Signal and power integrity - simplified", 2nd ed., Pearson, 2010
[2] Mutual Inductance and Capacitance Algorithm, rev. 01.8.2
[3] Adamczyk B. “EMC Crosstalk between PCB Traces”, West Michigan EMC Chapter Meeting, 2013
The article was first published in the journal "Components and Technologies" 2018, №4. The publication on Habr is coordinated with the editors of the journal.