Greetings to all, and especially those who are interested in the problems of discrete mathematics and graph theory.
Prehistory
It so happened that driven by interest, I was engaged in the development of the service of building a tour. routes. The task was to plan the best routes based on the city user of interest, the categories of establishments and the time frame. Well, one of the subtasks was to calculate travel time from one institution to another. Since I was young and stupid, I solved this problem head on with Dijkstra's algorithm, but it's fair to say that only with it you could run an iteration from one node to thousands of others, it was not an option to cache these distances; Moscow alone, and solutions like the Manhattan distance on our cities does not work at all from the word.
And so it turned out that the problem of productivity in the combinatorial problem was solved, but most of the time the request was eaten away by searching for uncached paths. The problem was complicated by the fact that the Osm road graph in Moscow is quite large (half a million nodes and 1.1 million arcs).
I will not talk about all the attempts and that in fact the problem could have been solved by cutting off the extra arcs of the graph, I’ll tell you only about the fact that at some point I was lit up and I realized that if I approach the Dijkstra algorithm from the point of view of the probabilistic approach, it can be linear.
Dijkstra for logarithmic time
Everyone knows, and it is not known to anyone, that the Dijkstra algorithm, by using a queue with logarithmic complexity of insertion and deletion, can lead to complexity of the form O (n log (n) + m log (n)). When using the Fibonacci heap, the complexity can be omitted to O (n * log (n) + m), but still not linear, but we would like.
In general, the queue algorithm is described as follows:
Let be:
- V is the set of vertices of the graph
- E - set of edges of the graph
- w [i, j] is the weight of the edge from node i to node j
- a - the initial top of the search
- q-vertex vertex
- d [i] - distance to the i-th node
- d [a] = 0, for all other d [i] = + inf
While q is not empty:
- v - vertex with minimum d [v] of q
- For all vertices u for which there is a transition to E from vertex v
- if d [u]> w [vu] + d [v]
- remove u from q with distance d [u]
- d [u] = w [vu] + d [v]
- add u to q with distance d [u]
- remove v from q
If a red-black tree is used as a queue, where insertion and deletion take place behind log (n), and the search for the minimum element is similar to log (n), then the complexity of the algorithm is O (n log (n) + m log (n)) .
And here it is worth noting one important feature: nothing prevents, in theory, to examine the top several times. If the vertex was considered and the distance to it was updated to an incorrect, larger than the true value, then provided that sooner or later the system converges and the distance to u is updated to the correct value, it is possible to do such tricks. But it is worth noting that one vertex should be viewed more than 1 time with some small probability.
Sorting hash table
To reduce the time of Dijkstra’s algorithm to linear, a data structure is proposed, which is a hash table with node numbers (node_id) as values. I note that the need for the array d does not go anywhere, it is still needed, that getting the distance to the i-th node in constant time.
The figure below shows an example of the work of the proposed structure.
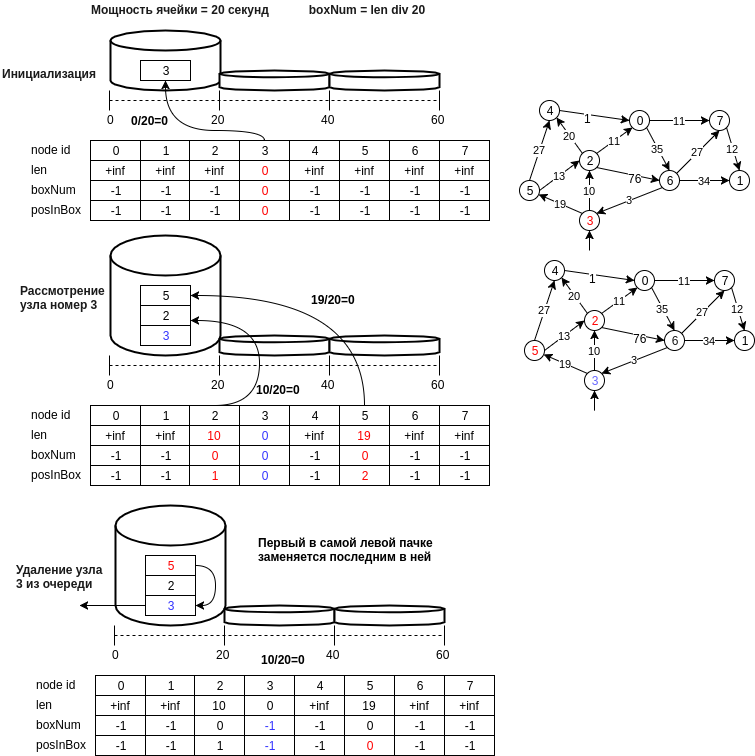
We describe in steps the proposed data structure:
- node u is written to the cell with the number equal to d [u] // bucket_size, where bucket_size is the cell power (for example, 20 meters, i.e. cell number 0 will contain nodes the distance to which will lie in the range [0, 20) meters )
- the minimum node will be the last node of the first non-empty cell, i.e. the operation of extracting the minimum element will be performed in O (1). It is necessary to maintain the current state of the identifier of the number of the first non-empty cell (min_el).
- The insert operation is performed by adding a new node number to the end of the cell and is also executed in O (1), since calculation of the cell number occurs in constant time.
- a delete operation, as in the case of a hash table, is a simple search, and one could make an assumption and say that with a small cell size this is also O (1). If you do not mind the memory (in principle, and not so much need, another array of n), then you can get an array of positions in the cell. In this case, if an element is deleted in the middle of a cell, it is necessary to move the last value in the cell to the place to be deleted.
- an important point when choosing the minimum element: it is minimal only with a certain probability, but, the algorithm will look at the min_el cell until it becomes empty and sooner or later the real minimum element will be considered, and if we accidentally update incorrectly the distance to the node reachable from minimum, then adjacent nodes with minimum can again be in the queue and the distance to them will be correct, etc.
- You can also delete empty cells up to min_el, thereby saving memory. In this case, the removal of the node v from the queue q should be done only after considering all adjacent nodes.
- and you can also change the power of the cell, the parameters for increasing the cell size and the number of cells when you need to increase the size of the hash table.
Measurement results
The checks were made on the osm map of Moscow, unloaded via osm2po in postgres, and then loaded into memory. Tests were written in Java. There were 3 versions of the graph:
- source graph - 0.43 million nodes, 1.14 million arcs
- compressed version of the graph with 173k nodes and 750k arcs
- the pedestrian version of the compressed version of the graph, 450k arcs, 100k nodes.
Below is a drawing with measurements on different versions of the graph:

Consider the dependence of the probability of re-viewing the vertex and the size of the graph:
| number of node views | number of vertices of the graph | the probability of re-viewing the site |
|---|
| 104915 | 100015 | 4.8 |
| 169429 | 167892 | 0.9 |
| 431490 | 419594 | 2.8 |
It can be noted that the probability does not depend on the size of the graph and is rather specific to the request, but small and its range is configured by changing the power of the cell. I would be very grateful for the help in building a probabilistic modification of the algorithm with parameters guaranteeing a confidence interval within which the probability of repeated viewing will not exceed a certain percentage.
Qualitative measurements were also carried out to practically confirm the comparison of the correctness of the result of the algorithms with the new data structure, which showed the complete coincidence of the shortest path length from 1000 random nodes to 1000 other random nodes on the graph. (and so 250 iterations) when working with a sorting hash table and a red-ebony tree.
The source code of the proposed data structure is by reference.
PS: I know about Torup’s algorithm and the fact that it solves the same problem in linear time, but I couldn’t manage this fundamental work in one evening, although I understood the idea in general terms. At least, as I understand it, a different approach is proposed there, based on the construction of a minimum spanning tree.
PSS During the week I will try to find time and make a comparison with the Fibonacci heap and add github repu with examples and test codes a little later.