Tupper's formula and implementation of the algorithm in Python

Instead of the preface

Not so long ago, on the Internet, I found out about such a wonderful and amazing copy of the Babylon Library as the Tupper formula . Rather, it is more Tupper's inequality than the formula. The peculiarity of this inequality is that it creates its own image on the graph. Just look at this miracle!

(Source Wikipedia)

What you see in the image is the formula of that same Jeff Tupper. Probably, half of the readers have already rushed in tungsten to draw the result of the implementation of this inequality ... But this is not so simple. As you can see in this image, the formula on the graph can be seen on the segment along the axis OY [k; k + 15]. What is this mysterious number k? Where do you get it? The thing is that this inequality, according to the concept of the Babylon Library, is able to display absolutely any image with a resolution of 106x17! Each image has its own position on the graph, thus, has a unique number k. Thus, for each number k there is a single image on the entire graph !

For this image, the number k looks like this:

4858450636189713423582095962494202044581400587983244549483093085061934704708809928450644769865524364849997247024915119110411605739177407856919754326571855442057210445735883681829823754139634338225199452191651284348332905131193199953502413758765239264874613394906870130562295813219481113685339535565290850023875092856892694555974281546386510730049106723058933586052544096664351265349363643957125565695936815184334857605266940161251266951421550539554519153785457525756590740540157929001765967965480064427829131488548259914721248506352686630476300

It is interesting to look at people who will scroll to such a coordinate in order to see the formula

I had the idea to write a program in Python3, which would allow to convert the image to the number k and vice versa and tell you about another excellent way to encode the image into a number.

Theory

(Added) How does this work?

Let's take a look at the formula itself:

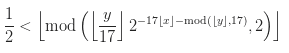
Let's define its syntax:

- the number rounded down
mod (x, y) is the remainder of dividing x by y

And then, it seems, everything is clear.
Note that both x and y are rounded down. It is this rounding that ultimately gives us a pixel image.

Denote everything that is rounded in the right side of the inequality for

$\ alpha$ .
Then

$1/2 <[\ alpha] <=> 1 <= [\ alpha]$

Which is obvious, because the whole expression is rounded down.

Let y = 17r + q, where r is the integer part of dividing y by 17, and r is the remainder of dividing. Thus, we in the formula can replace

$[y / 17]$ on r, and

$mod (y, 17)$ on q.

Get

$1 <= mod (q * 2 ^ {- 17-r}, 2)$

$1 <= mod (q / 2 ^ {17x + r}, 2)$

mod (

$\ alpha$ , 2) takes 2 values - 0 or 1. Accordingly, this inequality will say whether the number is

$q / 2 ^ {17x + r}$ even or not.

Note that the image is viewed on the interval [N, N + 16], respectively

$q = [y / 17]$ remains constant throughout the entire height of the image, which cannot be said about the number r (it varies from 0 to 16 throughout the entire image).

And now the cherry on the cake. Number

$[q / {2 ^ {17x + r}}]$ will be odd if and only if the bit under the number (17x + r) in the binary representation of the number q will be 1. And since the number q is constantly changing with the height and its binary representation too, we get a unique image every time! That’s how Tupper’s formula works.

Now let's see how to calculate the height at which we want to see our image.

The principle of calculating the number k

Tupper himself described the calculation of the number k for any image of size 106x17 (this is important!) As follows:

Convert image to black and white
Read each pixel from bottom to top, from left to right and put it in the buffer. If the pixel is black, then put 1, if white - 0.
Convert binary number to decimal and multiply by 17
Profit!

To get an image from number k, we do everything exactly the opposite. Well, let's go code!

Code

UPD: In the comments, people have slightly improved the code, made it simpler and more transparent. This article has published these updates. If you want to see old versions of the code, go to the githab repository (not yet zakomitil, link at the end of the article) and in the comments

From k to image

UPD

At the request of the commentators, a new way to calculate the image using this inequality and k! Now we will not do the manipulations with the number, transfer to the binary system, but directly affect the function itself!

Using the Tupper method to decode the number k

We get from the user the number k, ~~with closed eyes,~~ divide it by 17 and translate into a binary system.

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:]

We understand that some initial pixels may be white (equal to 0), respectively, in our binary number the first bits will be zeros, and when converting a number to a decimal system, these initial zeros will be lost. Therefore, we check the size of the binary number, if it is less than 1802, then we add zeros to the beginning.

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:] #   RadicalDreamer binary = ("0" * (1802 - len(binary))) + binary

Next, we will declare a two-dimensional list in which we will store information about each line of the image. Then we write there all the bits that have been read (do not forget the algorithm that creates the number k - bottom-up, left-to-right)

 lists = [[] for x in range(17)] #C   RadicalDreamer for x in range(1802): lists[-(x % 17)].append(binary[x]) <b> !</b> <source lang="python"> #-----!-----# image = Image.new("1", (106,17), (0)) # -  10617 draw = image.load() for y in range(17): for x in range(106): image.putpixel(xy=(105-x,16-y), value=(int(lists[y][x]),)) #    ,      lists image.save("image.png") #

Let's try to push the number k into our program, which I indicated at the beginning of the article, and we get the following:

As you can see, everything worked out for us, and we are now able to decode any k!

Using inequality to generate pictures from number k

First, we write the function in python:

 def f(x,y): return ((y//17)//(1 << (17*x+(y%17))))%2

Thanks to the // and << operators, the function implementation has been greatly simplified. It is guaranteed that the numbers x and y will be integers !

We again create a two-dimensional list, where we will store the bits of the image and write information about each line into it using cycles

 lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2))

And further, as in the previous example, we draw a picture using the PIL library.

Fully function looks like this:

 def from_k_to_bin(k: int) -> list: lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2)) return lists

Image in k

Well, now let's learn to encode any image into the number k.

First we get the image itself

 def get_image() -> Image: name = input("   (      ):") try: im = Image.open(name) except Exception: print("!") exit(0) return im

Check its size

 _SIZE_WIDTH = 106 _SIZE_HEIGHT = 17 image = get_image() width, height = image.size flag_okay = False if width == _SIZE_WIDTH and height == _SIZE_HEIGHT: flag_okay = True if not flag_okay: print("  ") print(width, height) exit(0) print(" !")

Make the image black and white and start reading pixel by pixel:

 image = image.convert('1') byteset = "" for x in range(105,-1,-1): for y in range(0,17): #c m03r   if image.getpixel((x,y)) > 127: byteset += '1' else: byteset += '0'

It remains only to convert to the decimal system and multiply by 17.

 k = int(byteset,2)*17 print(" :") print(k)

Well, let's go test!

I decided to code the habr logo. Here is the original image:

Run the program and specify the name of the image:

We got the following k:

4858487703217654168507377107565676789145697178497253677539145555247620343537955749299116772611982962556356527603203744742682135448820545638134012705381689785851604674225344958377377969928942310236199337805399065932982909660659786056259547094494380793146587709009524498386724160055692719747815828234655968636671461350354316223620304956111171025410498514602810746287134775641383930152393933036921599511277388743068766568352667661462097979110006690900253037600818522726237351439443865433159187625289316917268254866954663750093103703327097252478959

Let's check it out on our own program.

Here is the image we received: