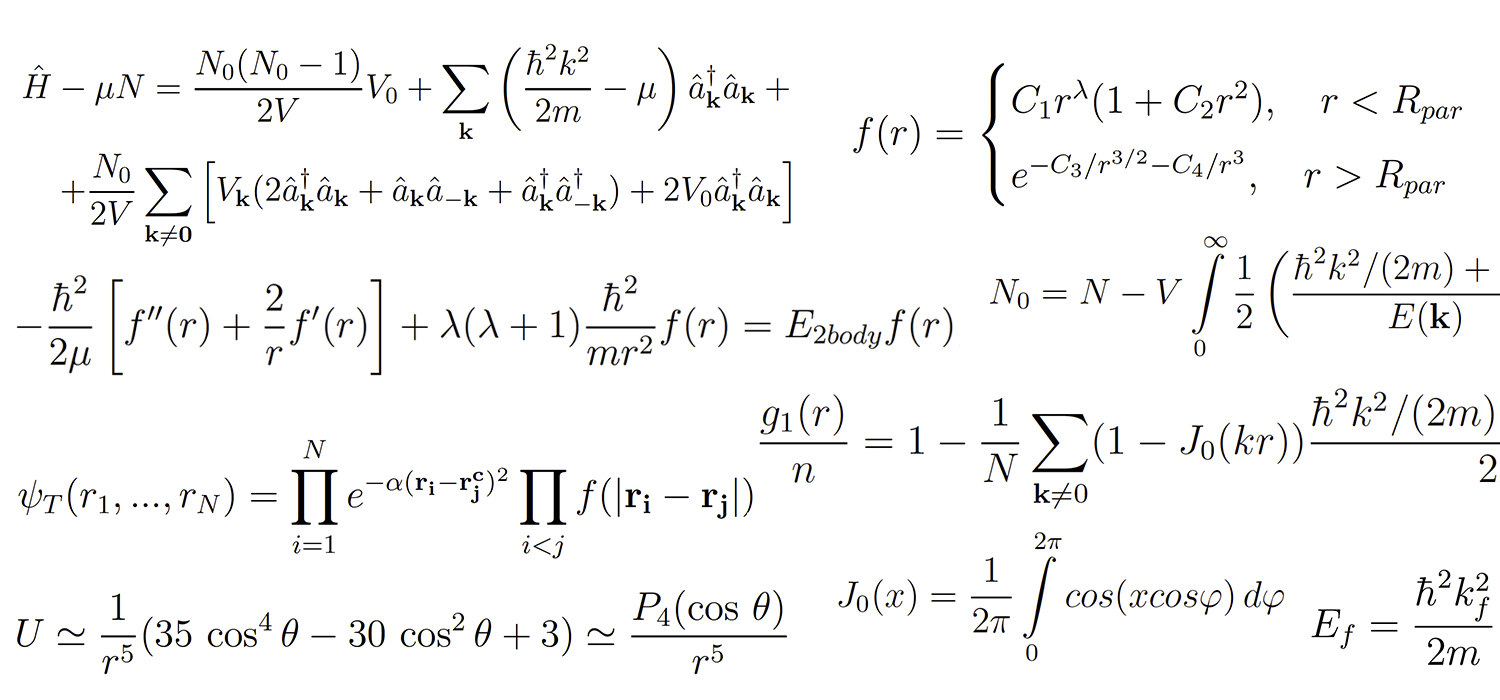
My specialty is condensed matter physics. Of course, in the process of immersion into it, it is required to study many scientific articles, however, at least one analysis can take a lot of time. On
arxiv, over a thousand articles per month are published in the
cond-mat section. There is a situation when many researchers, especially beginners, do not have a holistic vision of their field of science. The tool described in this article summarizes the contents of the scientific articles base and is intended to speed up the work with literature.
It is worth making a reservation that we are inventing a bicycle, only ours will ride for free (prices for
paid counterparts are so indecent that they are not taken to be indicated).
The bike will be built in Python,
Gensim is used for thematic modeling, and
Plot.ly is used for visualization. At the end of the article are links to Jupyter laptops and GitHub.
The source material for the work - annotations and texts of scientific articles. If the first ones are available to us in the “finished” XML form, then PDF files of articles need to be converted to txt, as a result of this process a lot of “garbage” remains in the texts, so they need to be seriously cleaned.
Sample annotation<?xml version="1.0" encoding="UTF-8"?> <feed xmlns="http://www.w3.org/2005/Atom"> <link href="http://arxiv.org/api/query?search_query%3D%26id_list%3D1706.09062%26start%3D0%26max_results%3D10" rel="self" type="application/atom+xml"/> <title type="html">ArXiv Query: search_query=&id_list=1706.09062&start=0&max_results=10</title> <id>http://arxiv.org/api/ECEwpFhuO79sa+LzMzx6/iStFak</id> <updated>2018-05-01T00:00:00-04:00</updated> <opensearch:totalResults xmlns:opensearch="http://a9.com/-/spec/opensearch/1.1/">1</opensearch:totalResults> <opensearch:startIndex xmlns:opensearch="http://a9.com/-/spec/opensearch/1.1/">0</opensearch:startIndex> <opensearch:itemsPerPage xmlns:opensearch="http://a9.com/-/spec/opensearch/1.1/">10</opensearch:itemsPerPage> <entry> <id>http://arxiv.org/abs/1706.09062v1</id> <updated>2017-06-27T22:03:24Z</updated> <published>2017-06-27T22:03:24Z</published> <title>On Bose-Einstein condensation and superfluidity of trapped photons with coordinate-dependent mass and interactions</title> <summary> The condensate density profile of trapped two-dimensional gas of photons in an optical microcavity, filled by a dye solution, is analyzed taking into account a coordinate-dependent effective mass of cavity photons and photon-photon coupling parameter. The profiles for the densities of the superfluid and normal phases of trapped photons in the different regions of the system at the fixed temperature are analyzed. The radial dependencies of local mean-field phase transition temperature $T_c^0 (r)$ and local Kosterlitz-Thouless transition temperature $T_c (r)$ for trapped microcavity photons are obtained. The coordinate dependence of cavity photon effective mass and photon-photon coupling parameter is important for the mirrors of smaller radius with the high trapping frequency, which provides BEC and superfluidity for smaller critical number of photons at the same temperature. We discuss a possibility of an experimental study of the density profiles for the normal and superfluid components in the system under consideration. </summary> <author> <name>Oleg L. Berman</name> </author> <author> <name>Roman Ya. Kezerashvili</name> </author> <author> <name>Yurii E. Lozovik</name> </author> <arxiv:doi xmlns:arxiv="http://arxiv.org/schemas/atom">10.1364/JOSAB.34.001649</arxiv:doi> <link title="doi" href="http://dx.doi.org/10.1364/JOSAB.34.001649" rel="related"/> <arxiv:comment xmlns:arxiv="http://arxiv.org/schemas/atom">14 page 5, figures</arxiv:comment> <link href="http://arxiv.org/abs/1706.09062v1" rel="alternate" type="text/html"/> <link title="pdf" href="http://arxiv.org/pdf/1706.09062v1" rel="related" type="application/pdf"/> <arxiv:primary_category xmlns:arxiv="http://arxiv.org/schemas/atom" term="cond-mat.mes-hall" scheme="http://arxiv.org/schemas/atom"/> <category term="cond-mat.mes-hall" scheme="http://arxiv.org/schemas/atom"/> </entry> </feed>
Sample textOn Bose-Einstein condensation and super¬‚uidity of trapped photons with
coordinate-dependent mass and interactions
Oleg L. Berman1,2, Roman Ya. Kezerashvili1,2, and Yurii E. Lozovik3,4
1Physics Department, New York City College of Technology, The City University of New York,
2The Graduate School and University Center, The City University of New York,
Brooklyn, NY 11201, USA
3Institute of Spectroscopy, Russian Academy of Sciences, 142190 Troitsk, Moscow, Russia
4National Research University Higher School of Economics, Moscow, Russia
New York, NY 10016, USA
(Dated: June 29, 2017)
The condensate density pro¬Ѓle of trapped two-dimensional gas of photons in an optical micro-
cavity, ¬Ѓlled by a dye solution, is analyzed taking into account a coordinate-dependent e¬Ђective
mass of cavity photons and photon-photon coupling parameter. The pro¬Ѓles for the densities of the
super¬‚uid and normal phases of trapped photons in the di¬Ђerent regions of the system at the ¬Ѓxed
temperature are analyzed. The radial dependencies of local mean-¬Ѓeld phase transition temperature
T 0
c (r) and local Kosterlitz-Thouless transition temperature Tc(r) for trapped microcavity photons
are obtained. The coordinate dependence of cavity photon e¬Ђective mass and photon-photon cou-
pling parameter is important for the mirrors of smaller radius with the high trapping frequency,
which provides BEC and super¬‚uidity for smaller critical number of photons at the same temper-
ature. We discuss a possibility of an experimental study of the density pro¬Ѓles for the normal and
super¬‚uid components in the system under consideration.
Key words: Photons in a microcavity; Bose-Einstein condensation of photons; super¬‚uidity of
photons.
PACS numbers: 03.75.Hh, 42.55.Mv, 67.85.Bc, 67.85.Hj
I.
INTRODUCTION
When a system of bosons is cooled to low temperatures, a substantial fraction of the particles spontaneously occupy
the single lowest energy quantum state. This phenomenon is known as Bose-Einstein condensation (BEC) and its
occurs in many-particle systems of bosons with masses m and temperature T when the de Broglie wavelength of the
Bose particle exceeds the mean interparticle distance [1]. The most remarkable consequence of BEC is that there
should be a temperature below which a ¬Ѓnite fraction of all the bosons ЂњcondenseЂќ into the same one-particle state
with macroscopic properties described by a single condensate wavefunction, promoting quantum physics to classical
time- and length scales.
Most recently, the observations at room temperature of the BEC of two-dimensional photon gas con¬Ѓned in an optical
microcavity, formed by spherical mirrors and ¬Ѓlled by a dye solution, were reported [2Ђ“5]. The interaction between
microcavity photons is achieved through the interaction of the photons with the non-linear media of a microcavity,
¬Ѓlled by a dye solution. While the main contribution to the interaction in the experiment, reported in Ref. 2, is
thermooptic, it is not a contact interaction.
It is known that BEC for bosons can exist without particle-particle
interactions [6] (see Ref. 1 for the details), but at least the interactions with the surrounding media are necessary to
achieve thermodynamical equilibrium. For photon BEC it can be achieved by interaction with incoherent phonons [7].
The in¬‚uence of interactions on condensate-number ¬‚uctuations in a BEC of microcavity photons was studied in Ref. 8.
The kinetics of photon thermalization and condensation was analyzed in Refs. 9Ђ“11. The kinetics of trapped photon
gas in a microcavity, ¬Ѓlled by a dye solution, was studied, and, a crossover between driven-dissipative system laser
dynamics and a thermalized Bose-Einstein condensation of photons was observed [12].
In previous theoretical studies the equation of motion for a BEC of photons con¬Ѓned by the axially symmetrical
trap in a microcavity was obtained.
It was assumed that the changes of the cavity width are much smaller than
the width of the trap [13]. This assumption results in the coordinate-independent e¬Ђective photon mass mph and
photon-photon coupling parameter g. In this Paper, we study the local super¬‚uid and normal density pro¬Ѓles for
trapped two-dimensional gas of photons with the coordinate-dependent e¬Ђective mass and photon-photon coupling
parameter in a an optical microcavity, ¬Ѓlled by a dye solution. We propose the approach to study the local BEC
and local super¬‚uidity of cavity photon gas in the framework of local density approximation (LDA) in the traps of
larger size without the assumption, that total changes of the cavity width are much smaller than the size of the trap.
In this case, we study the e¬Ђects of coordinate-dependent e¬Ђective mass and photon-photon coupling parameter on
the super¬‚uid and normal density pro¬Ѓles as well as the pro¬Ѓles of the local temperature of the phase transition for
trapped cavity photons. Such approach is useful for the mirrors of smaller radius with the high trapping frequency,
2
which provide BEC and super¬‚uidity for smaller critical number of photons at the same temperature.
The paper is organized in the following way.
In Sec. II, we obtain the condensate density pro¬Ѓle for trapped
microcavity photon BEC with locally variable mass and interactions. The expression for the number of particles in a
condensate is analyzed in Sec. III. In Sec. IV, the dependence of the condensate parameters on the geometry of the
trap is discussed. In Sec. V, we study the collective excitation spectrum and super¬‚uidity of 2D weakly-interacting
Bose gas of cavity photons. The results of our calculations are discussed in Sec. VI. The proposed experiment for
measuring the distribution of the local density of a photon BEC is described in Sec. VII. The conclusions follow in
Sec. VIII.
II. THE CONDENSATE DENSITY PROFILE
While at ¬Ѓnite temperatures there is no true BEC in any in¬Ѓnite untrapped two-dimensional (2D) system, a true
2D BEC quantum phase transition can be obtained in the presence of a con¬Ѓning potential [14, 15]. In an in¬Ѓnite
translationally invariant two-dimensional system, without a trap, super¬‚uidity occurs via a Kosterlitz€'Thouless
super¬‚uid (KTS) phase transition [16]. While KTS phase transition occurs in systems, characterized by thermal
equilibrium, it survives in a dissipative highly nonequilibrium system driven into a steady state [17].
The trap for the cavity photons can be formed by the concave spherical mirrors of the microcavity, that provide
the axial symmetry for a trapped gas of photons. Thus the transverse (along xy plane of the cavity) con¬Ѓnement
of photons can be achieved by using an optical microcavity with a variable width. Let us introduce the frame of
reference, where z€'axis is directed along the axis of cavity mirrors, and (x, y) plane is perpendicular to this axis. The
energy spectrum E(k) for small wave vectors k of photons, con¬Ѓned in z direction in an ideal microcavity with the
coordinate-dependent width L(r), is given by [2]
E(k) =
ЇhЂcњn
...
[23] L. Onsager, ЂњStatistical Hydrodynamics,Ђќ Nuovo Cimento Suppl. 6, 279 (1949).
[24] RP Feynman, ЂњApplication of Quantum Mechanics to Liquid Helium,Ђќ Prog. Low Temp. Phys. 1, 17 (1955).
[25] PC Hohenberg and PC Martin, ЂњMicroscopic Theory of Super¬‚uid Helium,Ђќ Ann. Phys. 34, 291 (1965).
[26] G. Blatter, MY FeigelЂman, YB Geshkenbein, AI Larkin, and VM Vinokur, ЂњVortices in high-temperature super-
conductors,Ђќ Rev. Mod. Phys. 66, 1125 (1994).
[27] NS Voronova and Yu. E. Lozovik, ЂњExcitons in cores of exciton-polariton vortices,Ђќ Phys. Rev. B 86, 195305 (2012);
NS Voronova, AA Elistratov, and Yu. E. Lozovik, ЂњDetuning-Controlled Internal Oscillations in an Exciton-Polariton
Condensate,Ђќ Phys. Rev. Lett. 115, 186402 (2015) .
[28] A. Gri¬ѓn, ЂњConserving and gapless approximations for an inhomogeneous Bose gas at ¬Ѓnite temperatures,Ђќ Phys. Rev. B
53, 9341 (1996).
[29] AA Abrikosov, LP Gorkov and IE Dzyaloshinski, Methods of Quantum Field Theory in Statistical Physics (Prentice-
Hall, Englewood Cli¬Ђs. NJ, 1963).
[30] OL Berman, Yu. E. Lozovik, and DW Snoke, ЂњTheory of Bose-Einstein condensation and super¬‚uidity of two-
dimensional polaritons in an in-plane harmonic potential,Ђќ Phys. Rev. B 77, 155317 (2008).
[31] OL Berman, R. Ya. Kezerashvili, and K. Ziegler, ЂњSuper¬‚uidity and collective properties of excitonic polaritons in gapped
graphene in a microcavityЂќ, Phys. Rev. B 86, 235404 (2012).
[32] A. Amo, J. Lefr`ere, S. Pigeon, C. Adrados, C. Ciuti, I. Carusotto, R. Houdrґe, E. Giacobino, and A. Bramati, ЂњSuper¬‚uidity
of polaritons in semiconductor microcavities,Ђќ Nature Physics 5, 805 (2009).
[33] JP Fernґandez and WJ Mullin, ЂњThe Two-Dimensional Bose€'Einstein Condensate,Ђќ J. Low. Temp. Phys. 128, 233
From the annotations we need information
only about the authors and subsections of the articles.
Below, as an example, we consider an array of articles from the cond-mat section for 2017. Everything described is easy to reproduce for any other section.
The simplest way to start researching texts is to make a list of keywords of interest to us and calculate the percentage of articles in which they are found.
Let us estimate the change in share, for example, compared to 2010.
The difference in shares for the 2017th and 2010th years. (approx .: Nobel Prize in Physics in 2016 was awarded for the study of topological phases of matter)Next, based on the content of the texts we build the
word2vec model (for visualization, it is better to take a window wider, 20 words). For each key, we take N nearest neighbors and with the help of t-SNE we calculate their 2D coordinates. We look at how keywords relate to each other:
Cloud keywords and their satellites, N = 100. The further the Nth neighbor is, the more the word is highlighted. Relevant pairs: Graphene + Semiconductor, Qubit + Dot, Topological + Hall, Bose + CondensationOn arxiv for each section there are subsections. We find out in which subsections the keywords are found:
Deciphering the names of subdivisions cond-matThe above describes how to work with a set of keywords that you need to compile manually, but some topics could be skipped. Let's build an
LDA model and look at the topics:
For each topic, we get a list of the corresponding articles:
As you know, when reading articles it is always useful to examine the links. Can we collect some information about them? We can! Let's look at the "tail" of the text.
Tail[23] L. Onsager, ЂњStatistical Hydrodynamics,Ђќ Nuovo Cimento Suppl. 6, 279 (1949).
[24] RP Feynman, ЂњApplication of Quantum Mechanics to Liquid Helium,Ђќ Prog. Low Temp. Phys. 1, 17 (1955).
[25] PC Hohenberg and PC Martin, ЂњMicroscopic Theory of Super¬‚uid Helium,Ђќ Ann. Phys. 34, 291 (1965).
[26] G. Blatter, MY FeigelЂman, YB Geshkenbein, AI Larkin, and VM Vinokur, ЂњVortices in high-temperature super-
conductors,Ђќ Rev. Mod. Phys. 66, 1125 (1994).
[27] NS Voronova and Yu. E. Lozovik, ЂњExcitons in cores of exciton-polariton vortices,Ђќ Phys. Rev. B 86, 195305 (2012);
NS Voronova, AA Elistratov, and Yu. E. Lozovik, ЂњDetuning-Controlled Internal Oscillations in an Exciton-Polariton
Condensate,Ђќ Phys. Rev. Lett. 115, 186402 (2015) .
[28] A. Gri¬ѓn, ЂњConserving and gapless approximations for an inhomogeneous Bose gas at ¬Ѓnite temperatures,Ђќ Phys. Rev. B
53, 9341 (1996).
[29] AA Abrikosov, LP Gorkov and IE Dzyaloshinski, Methods of Quantum Field Theory in Statistical Physics (Prentice-
Hall, Englewood Cli¬Ђs. NJ, 1963).
[30] OL Berman, Yu. E. Lozovik, and DW Snoke, ЂњTheory of Bose-Einstein condensation and super¬‚uidity of two-
dimensional polaritons in an in-plane harmonic potential,Ђќ Phys. Rev. B 77, 155317 (2008).
[31] OL Berman, R. Ya. Kezerashvili, and K. Ziegler, ЂњSuper¬‚uidity and collective properties of excitonic polaritons in gapped
graphene in a microcavityЂќ, Phys. Rev. B 86, 235404 (2012).
[32] A. Amo, J. Lefr`ere, S. Pigeon, C. Adrados, C. Ciuti, I. Carusotto, R. Houdrґe, E. Giacobino, and A. Bramati, ЂњSuper¬‚uidity
of polaritons in semiconductor microcavities,Ђќ Nature Physics 5, 805 (2009).
[33] JP Fernґandez and WJ Mullin, ЂњThe Two-Dimensional Bose€'Einstein Condensate,Ђќ J. Low. Temp. Phys. 128, 233
The PDF converter handles the bibliography section well. This means that links can be extracted with a few regular expressions. As a result, we get a list of frequently cited, must-read articles.
Check these links in
Google Scholar :
Make a list of the most active authors for each subsection - extract and calculate the contents of the author tag from the annotations. The number of articles published by a particular author is a characteristic that is clear but unreliable, it can be supplemented with a median number of co-authors (see laptops).
Authors from mes-hall are out of competition: their average work rate is more than one article per week ...Finally, we estimate the share of subsections:
Demo laptops:
cond-mat.17 ,
astro-ph.17 ,
cs.17 ,
math.17GitHub:
ilovescience