The dynamics of the vertical flight of the aircraft lighter than air

Introduction

Determining the speed of lifting and lowering aircraft lighter than air (LALV) to date is practically an important task arising in the design of such devices.

A large number of publications devoted to LALV, for example, only on our resource are two very interesting articles [1, 2] concerning the history of development on the example of specific designs of airships and stratostats. However, very few calculations of the dynamics of the vertical flight of such devices, allowing at least tentatively determine the speed of ascent and descent LALV.

The last statement requires a certain explanation, since the sophisticated reader well remembers a school course in physics, in which problems were solved for lift height and other parameters of balloons filled with gases lighter than air or with air itself heated during flight.

All of these tasks were based on the equality of two forces: the force of weight and buoyancy. Gases were considered ideal and their parameters were calculated according to the Mendeleev Clapeyron law. However, even a simple accounting for the third air resistance force already leads to a system of differential equations that cannot be solved analytically. It is also necessary to take into account the change in the density of atmospheric air with a height of rise and temperature.

In addition, if you need to consider not only lifting, but also the hanging of the ball and its descent to the ground, then this is not a child’s task at all. I hope that consideration of the solution of a similar problem using Python tools will not only contribute to the expansion of knowledge in physics, but also popularize the Python programming language itself. What I am trying to do in my publications on this resource.

Mathematical model of the flight LALV with a shell in the form of a ball, the volume of which does not change with height

We confine ourselves to considering the movement of its center of mass under the action of the following forces: gravity ( G ), Archimedean force ( Fa ) and aerodynamic drag force ( Fc ). We write the correlation to determine the forces through the parameters of motion and air [3]:

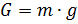
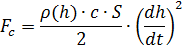
In the above formulas, the following designations are used: h is the height of the ball, dh / dt is the vertical speed, m is the mass, g is the acceleration of free fall, W is the volume of the ball, c is the drag coefficient, S is the characteristic area of resistance (area of the mid-section).
The dependence of air density on height will be considered exponential:

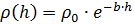
Where

ρ_{0}

$ρ_0$ - air density at zero height, b – coefficient. The force of gravity is directed downwards, the Archimedean force is directed upwards, and the force of aerodynamic drag is always directed “against the movement”, therefore, the correct consideration of this force in the equations of motion requires the introduction of a multiplier

- s i n g (d h / d t)

$-sing (dh / dt)$ .

However, for our purposes this fact is not of fundamental importance, and we will limit ourselves to considering only the stage of lifting the ball when the force of aerodynamic drag is directed downwards and, therefore, will be taken into account in the equations of motion with a minus sign. Now the equation of motion can be written in the form:

, (one)

Additionally assume that the balloon is a homogeneous body of radius R with density

ρ_{b}

$ρ_b$ . Then the size of the area, which determines its aerodynamic resistance, will be defined as

volume as

and mass, respectively, as

.

Now it is clear that each term of equation (1) contains the value of S as a multiplier. Therefore, each term of the equation of motion can be reduced by the value of the factor S, and the equation itself takes the form:

, (2)

We introduce the notation:

;

;

and rewrite (2) in the form of the following system of nonlinear equations:

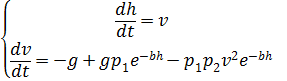
, (3)

Influence on the speed and height of LALV air temperature rise

To do this, first solve the system (3) using the following relationship for the dependence of the density of atmospheric air on height without taking into account the temperature

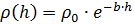
We repeat the solution of the system (3), but using the relationship for the dependence of air density on height and temperature:

where: b = 0.000125 is a constant related to air density of 1 / m;
a = 0.0065 is a constant related to air temperature in K / m.

T_{0} = 300 K

$T_0 = 300 K$ - temperature at sea level.

Program listing

# -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#       /2. rv=1.29#     /3. rg=0.17#    /3. R=8#     . b=0.000125# ,      1/ a=6.5*10**-3# ,      / c=0.4#   mo=240#   V=(4/3)*pi*R**3 rs=rg+mo/V#    ,  ,   p1=rv/rs#   p2=3*c/(8*R)#   T0=300 def fun(y, t): y1, y2= y return [y2,-g+g*p1*exp(-b*y1*T0/(T0-a*y1))-p1*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] t =arange(0,1100,0.01) y0 = [0.0,0.0] [y1,y2]=odeint(fun, y0,t, full_output=False).T plt.title("   \n : %s 3.  : %s . \n  : %s k. "%(round(V,0),mo,round(0.001*g*rv*V,0))) plt.plot(t/60,y1,label='  : %s . \n  : % s / .\n    '%(round(max(y1)/1000,2),round(max(y2),2))) def fun(y, t): y1, y2= y return [y2,-g+g*p1*exp(-b*y1)-p1*p2*exp(-b*y1)*y2**2] [y1,y2]=odeint(fun, y0,t, full_output=False).T plt.plot(t/60,y1,label='  : %s . \n  : % s / \n    '%(round(max(y1)/1000,2),round(max(y2),2))) plt.ylabel('  ') plt.xlabel('   ') plt.legend(loc='best') plt.grid(True) plt.show()

We get:

The calculated value of the height of the lift LALV taking into account the temperature is less than without taking into account. The lifting speed of the device at the same time remains unchanged.

Characterization of all phases of the LALV flight from start to landing

To build the LALV flight program, consider the conditions for the following time periods:

Rise -

;
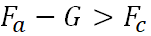
Hang -

;
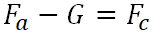
Landing -

Program listing

 # -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#       /2. rv=1.29#     /3. rg=0.17#    /3. R=8#     . b=0.000125# ,      1/ a=6.5*10**-3# ,      / c=0.4#    mo=240#    V=(4/3)*pi*R**3 p2=3*c/(8*R)#   T0=300#     tz=4000#     rgu=1.2#         /3 tz=4000#   def fun(y, t): y1,y2= y if y2<=0: if t<tz: return [y2,-g+g*(rv/(rg+mo/V))*exp(-b*y1*T0/(T0-a*y1))+(rv/(rg+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] elif t>=tz: return [y2,-g+g*(rv/(rgu+mo/V))*exp(-b*y1*T0/(T0-a*y1))+(rv/(rgu+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] else: return [y2,-g+g*(rv/(rg+mo/V))*exp(-b*y1*T0/(T0-a*y1))-(rv/(rg+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] t =arange(0,tz+555,0.1) y0 = [0.0,0.0] [y1,y2]=odeint(fun, y0,t, full_output=False).T plt.title(", ,   \n      \n : %s 3.  : %s .  : %s k. "%(round(V,0),mo,round(0.001*g*rv*V,0))) plt.plot(t,y1,label='  : %s . \n  : % s / .\n   %s .'%(round(max(y1)/1000,2), round(max(y2),2),tz-2*555)) plt.ylabel('  ') plt.xlabel('   .') plt.legend(loc='best') plt.grid(True) plt.show()

We get:

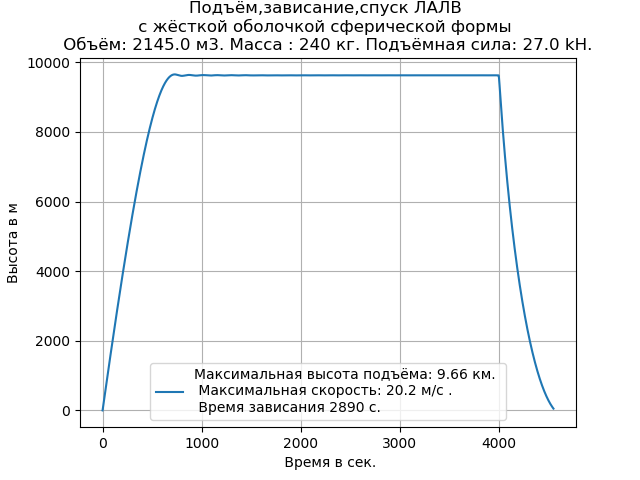
As follows from the given schedule and program listing, for carrying out a computational experiment it is enough to enter the necessary initial data.

Mathematical model of the flight LALV with a shell, the volume of which varies with altitude

Such LALV are stratostatics. The stratostat cannot be completely inflated with helium, giving it maximum lifting force, which will transform the shape of its shell into a ball. Such a ball at high altitude may burst under the action of the increased difference between the internal and external pressures.

For these reasons, for calculating the maximum attainable lift height, two values of its volume are introduced: the minimum Vmin and the maximum Vmax, respectively. Taking into account the variables introduced and the dependence of air density on the height of the ratio for the buoyancy force Fa and gravity Ft will take the form:

, (four)

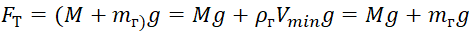
, (five)

where: M is the mass of the shell and equipment of the stratostat;

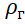
- helium density.

Equating relations (4) and (5), assuming that the volume of the shell V is a function of the lifting height LALV, we obtain the relation:

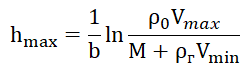
. (6)

The numerical values of the parameters included in the relation (6) are given in the listing for plotting, which is provided only for the specified purpose.

Listing a chart with data

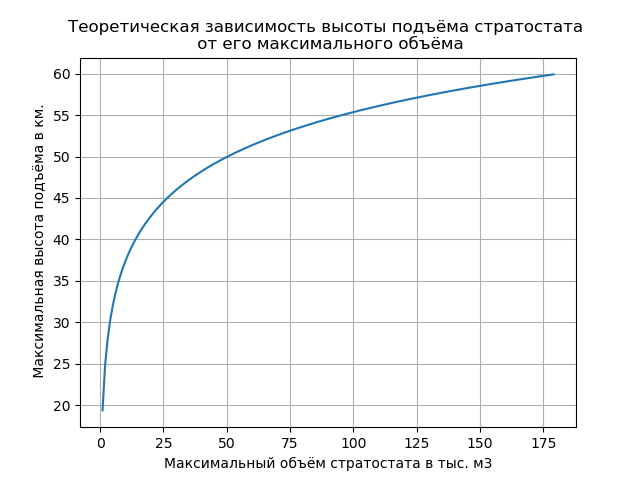
 # -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#       /2. rv=1.29#     /3. rg=0.17#    /3. Vmin=400#    /3. b=0.000128# ,      1/. c=0.8#   mo=40#   rs=rg+mo/Vmin#    ,     p1=rv/rs#   h=[(10**-3)*log((rv*w)/(mo+rg*Vmin))*b**-1 for w in arange(1*10**3,1.8*10**5,1000)] v=[(10**-3)*w for w in arange(1*10**3,1.8*10**5,1000)] plt.title("     \n    ") plt.plot(v,h) plt.xlabel('    . 3') plt.ylabel('     .') plt.grid(True) plt.show()

We get:

By changing the LALV parameters given in the program listing, one can obtain the given graph and select the required maximum shell volume during design. Refinement of the results carried out with the use of vast experience in the creation of such devices.

Findings:

Mathematical models of two types of aircraft lighter than air have been obtained, which allow computational experiments to be carried out for estimating the parameters of such devices under idealized conditions of the air environment.
The proposed multi-stage scheme for the numerical solution of a system of differential equations makes it possible to obtain a vertical trajectory of aircraft lighter than air at the stages of lifting the hang and descent.

The dynamics of the vertical flight of the aircraft lighter than air

Introduction

Mathematical model of the flight LALV with a shell in the form of a ball, the volume of which does not change with height

Influence on the speed and height of LALV air temperature rise

Characterization of all phases of the LALV flight from start to landing

Mathematical model of the flight LALV with a shell, the volume of which varies with altitude

Links

More articles: