In this series of articles you will learn about the basic principles of functional programming and understand what it means to “think functionally” and how this approach differs from object-oriented or imperative programming.

Now that you have seen some of the reasons for using F #, see the article Immersion in F #. A Handbook for C # Developers , take a step back and discuss the basics of functional programming. What does “functionally functionally” mean, and how does this approach differ from object-oriented or imperative programming?
Changing the way of thinking (Intro)
It is important to understand that functional programming is not just a separate programming style. This is a completely different way of thinking in programming, which differs from the “traditional” approach as much as the current OOP (in the Smalltalk style) differs from the traditional imperative language, such as C.
F # allows non-functional coding styles to be used, and this tempts the programmer to preserve his existing habits. In F #, you can program as you are accustomed to, without changing radically the worldview, and not even imagining what you are missing. However, in order to get the most out of F #, and also to learn how to confidently program in a functional style in general, it is very important to learn to think functionally, and not imperatively.
The purpose of this series of articles is to help the reader understand the background of functional programming and change his way of thinking.
This will be a rather abstract series, although I will use many short code examples to demonstrate some of the points. We will cover the following topics:
- Mathematical functions . The first article introduces the mathematical concepts underlying functional languages and the advantages that this approach brings.
- Functions and Values . The following introduces functions and values, explains how “values” differ from variables, and what are the similarities between functions and simple values.
- Types . Then we move on to the main types that work with functions: primitive types, such as string and int, type unit, functional types, and generic types.
- Functions with multiple parameters . Next, I will explain the concept of "currying" and "partial application." In this place, someone's brain will hurt, especially if these brains only have an imperative past.
- Definition of functions . Then several posts will be devoted to many different ways of defining and combining functions.
- Signatures of functions . Next, there will be an important post about the critical meaning of function signatures, what they mean, and how to use signatures to understand the contents of functions.
- The organization of functions . When it becomes clear how to create functions, the question will arise: how can they be organized to be accessible to the rest of the code?
Mathematical functions
Functional programming is inspired by mathematics. Mathematical functions have a number of very nice features that functional languages are trying to implement.
Let's start with a mathematical function that adds 1 to the number.
Add1(x) = x+1
What does this expression really mean? Looks pretty simple. It means that there is an operation that takes a number and adds 1 to it.
Let's add some terminology:
- The set of valid input values for the function are called domain (domain). In this example, it could be a set of real numbers, but let's make life easier and confine ourselves here to whole numbers.
- The set of possible results of a function (range of values) is called range (technically, the image is codomain ). In this case, also many integers.
- A function is a map (in the original map ) from a domain in range. (Ie from the domain of definition to the domain of values.)
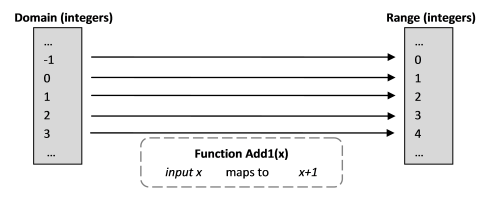
This is what the definition would look like on F #.
let add1 x = x + 1
If you enter it in F # Interactive (do not forget about double semicolons), then you can see the result (the "signature" of the function):
val add1 : int -> int
Consider the output in detail:
- The general meaning is that the
add1 function associates integers (from the domain of definition) with integers (from the domain of values). - “
add1 ” is defined as “val”, short for “value”. Hm what does it mean? We will discuss the meanings later. - The "->" arrow notation is used to show the domain and range. In this case, domain is a type of 'int', as well as range.
Notice that the type was not specified explicitly, but the F # compiler decided that the function works with ints. (Can this be changed? Yes, and soon we will see it).
Key properties of mathematical functions
Mathematical functions have a number of properties that distinguish them very much from functions that are used in procedural programming.
- A function always has the same result for the same input value.
- The function has no side effects.
These properties provide a number of noticeable advantages that functional programming languages try to implement as much as possible in their design. Consider each of them in turn.
Mathematical functions always return the same result for a given value.
In imperative programming, we think that functions either “do” something, or “count” something. Mathematical functions do not consider anything; they are pure mappings from input to output. In fact, another definition of a function is a simple set of all mappings. For example, you can very roughly define the function '' add1 '"(in C #) as
int add1(int input) { switch (input) { case 0: return 1; case 1: return 2; case 2: return 3; case 3: return 4; etc ad infinitum } }
Obviously, it is impossible to have a case for each possible number, but the principle is the same. With this formulation, no calculations are performed; only a search is performed.
Mathematical functions are free from side effects.
In a mathematical function, the input and output values are logically two different things, both of which are predefined. The function does not change the input or output data and simply maps the predefined input value from the definition domain to the predefined output value in the value domain.
In other words, the calculation of the function can not have any effects on the input data or anything else of the kind . It should be remembered that the calculation of the function does not actually consider and does not manipulate anything, it is just a search of a laud.
This “immobility” of values is very subtle, but at the same time very important thing. When I do math, I don’t expect the numbers to change as they are added. For example, if I have given:
x = 5 y = x+1
Then I do not expect x change when I add 1 to it. I expect to get another number ( y ), and x should remain intact. In the world of mathematics, integers already exist in an immutable set, and the function "add1" simply defines the relationship between them.
The power of pure functions
Those types of functions that have repeatable results and have no side effects are called "pure / pure functions", and with them you can do some interesting things:
- They are easy to parallelize. Say, we could take whole numbers in the range from 1 to 1000 and distribute them to 1000 different processors, and then assign each CPU to perform "
add1 " on the corresponding number, while being sure that there is no need for any interaction between them. No locks, no mutexes, no semaphores, etc. - You can use functions lazily, calculating them when necessary for program logic. You can be sure that the answer will be exactly the same, regardless of whether the calculations are performed now or later.
- It is possible to carry out calculations of the function for a particular input only once, and then cache the result, because it is known that these input values will give the same output.
- If there are many pure functions, they can be calculated in any order. Again, this cannot affect the final result.
Accordingly, if the programming language has the ability to create pure functions, you can immediately get a lot of powerful techniques. And undoubtedly, all this can be done in F #:
- An example of parallel computing was in the series “Why use F #?” .
- Lazy evaluation of functions will be discussed in the Optimization series .
- The caching of function results is called memoization and will also be discussed in the “Optimization” series .
- The absence of the need to track the execution order makes parallel programming much easier and allows you not to encounter bugs caused by changing the order of functions or refactoring.
"Useless" properties of mathematical functions
Mathematical functions also have some properties that seem not very useful when programming.
- Input and output values are immutable
- Functions always have one input and one output.
These properties are reflected in the design of functional programming languages. It is worth considering them separately.
Input and output values are immutable
Immunable values in theory seem like a good idea, but how can you really do any work if you cannot assign a variable in the traditional way.
I can assure you that this is not such a big problem as you can imagine. In the course of this series of articles, it will be clear how this works in practice.
Mathematical functions always have one input and one output.
As can be seen from the diagrams, for a mathematical function there is always only one input and only one output. This is also true for functional programming languages, although it may not be obvious when first used.
This seems like a big inconvenience. How can you do something useful without functions with two (or more) parameters?
It turns out that there is a way to do this, and moreover, it is absolutely transparent to F #. It is called "currying", and deserves a separate post, which will appear in the near future.
In fact, it will later become clear that these two “useless” properties will become incredibly valuable, and will be the key part that makes functional programming so powerful.
Additional resources
For F #, there are many tutorials, including materials for those who come with C # or Java experience. The following links may be helpful as you learn more about F #:
Several other ways to get started with learning F # are also described.
Finally, the F # community is very friendly to beginners. There is a very active Slack chat, supported by the F # Software Foundation, with rooms for beginners that you can freely join . We strongly recommend that you do this!
Do not forget to visit the site of the Russian-speaking community F # ! If you have any questions about learning the language, we will be happy to discuss them in chat rooms:
About authors of translation
Translated by @kleidemos
 Translation and editorial changes are made by the efforts of the Russian-speaking community of F # -developers . We also thank @schvepsss and @shwars for preparing this article for publication.
Translation and editorial changes are made by the efforts of the Russian-speaking community of F # -developers . We also thank @schvepsss and @shwars for preparing this article for publication.