Irregular tiles on the surface of procedurally generated planets

Here we will consider the method of dividing a spherical surface of a procedurally-generated planet with irregular tiles, and, as its consequence, the division of the ocean and continents into separate sectors (sectors). We assume that the structure of land areas on the surface of the planet is already defined using any GIS and it is possible to export vector data to ESRI shapefiles or directly to PostgreSQL database with PostGIS extension. The process of creating sectors is carried out by means of PostGIS.

See the link to the script with SQL code at the bottom of the post, here the explanation will be more on-the-fingers. The explanation provides the main functions from the script, and also assumes the availability of data for continents and rivers of procedurally-generated planets taken from forgedmaps.com .

The choice of irregular tiles allows us to precisely subdivide the surface of the planet.
on the sector, generally nowhere mixing the territory of the ocean and land. Lakes and inland seas
we consider here part of sushi. We will also see how rivers can be used as natural sector boundaries. The sectors themselves will be built on the basis of some basic division of the sphere by polygons.

When it comes to the division of a flat area, usually, to obtain irregular tiles, resort to the Voronoi diagram . Using, also, the Lloyd's algorithm , one can come to a visually attractive form of convex polygons that do not differ much in size (Centroidal Voronoi tessellation). The essence of Lloyd’s algorithm is to repeat the construction of the Voronoi diagram, taking the centers of polygons obtained at the previous iteration as generating points.

We will impose certain requirements on the basic division of polygons of the sphere:
convexity of spherical polygons and not very large deviations from a given average size.

The name of the sector is used instead of a tile , because a tile usually has an elementary meaning, for example, as a single part of the tile cards of strategic games, or as a single part of a certain surface. Inside the sector there is an internal structure: relief and various geographical objects in it. Sectors, in turn, can also serve as elementary tiles: this goal is served by constructing a graph of possible transitions between sectors.

The basic division of the sphere and segments of the oceans.

In PostGIS there is a function ST_VoronoiPolygons , which builds a Voronoi diagram in a square domain. Let's see how we can use it for our purposes.

What happens if you try to use a straightforward approach? Any rectangular projection of the planet can be transformed by coordinates to a square, build polygons there and perform the inverse transformation of coordinates. But the rectangles thus constructed will be drawn in one direction, which would be undesirable. And if you try to apply the Lloyd algorithm, the rectangles close to the poles of the sphere will be significantly smaller in area (on the sphere) than close to the equator.

Let's try to adapt this method with the elimination of deficiencies. The random initial points of the Voronoi diagram are chosen so that they are evenly distributed on the sphere. In the Mercator projection, this means that to the poles they should appear less frequently with a probability proportional to the cosine of latitude. We construct the Voronoi diagram in the "world" polygon, this is either the entire rectangular projection of the planet or only part of it. The ST_VoronoiPolygons function itself completes the rectangle to a square, we only need to cut the resulting diagram along the “world” polygon.

We look at the picture of the Voronoi polygons obtained by the adapted method. Here is a portion of the map of the test planet from the equator at the upper edge to 73 degrees south latitude at the lower edge. (Here the land area has already been cut out of polygons.)



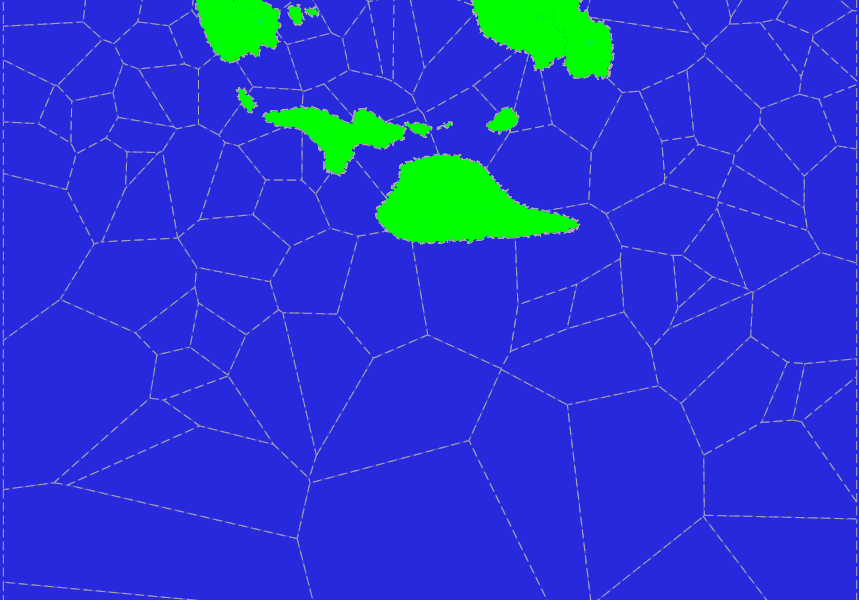
As can be seen on the Mercator projection, polygons are usually larger when approaching the poles, but on a sphere they will be approximately equally distributed over the area. That's what we need. But, it is also clear that the polygons have a very large spread of areas and the overall picture is rather unattractive.

Let's try to apply several iterations of the Lloyd's algorithm. As new points
for subsequent iterations of the Voronoi diagram we will choose the centers of the already cut off
"World" polygon Voronoi polygons. And, in order to prevent too large a decrease in polygon areas near the poles, we only do a small number of iterations (3 or so).

To obtain ocean segments from landfill sites, the land area is excluded. As a result, polygons of small size can be formed, which it is desirable to attach to the neighboring ones. Also, small polygons may be near the border of the "world" polygon. Joining polygons is done in such a way as to select the “nearest” neighbor and not to spoil the big picture.

After applying such a modified algorithm, we obtain the following picture, which may already be acceptable. Red lines in the figure indicate the desired merging of polygons.



The selection of polygons to merge can be done in different ways. In the above script, two methods are implemented: along the longest border and along the nearest center. The following figure shows the result of the merge in the second method.



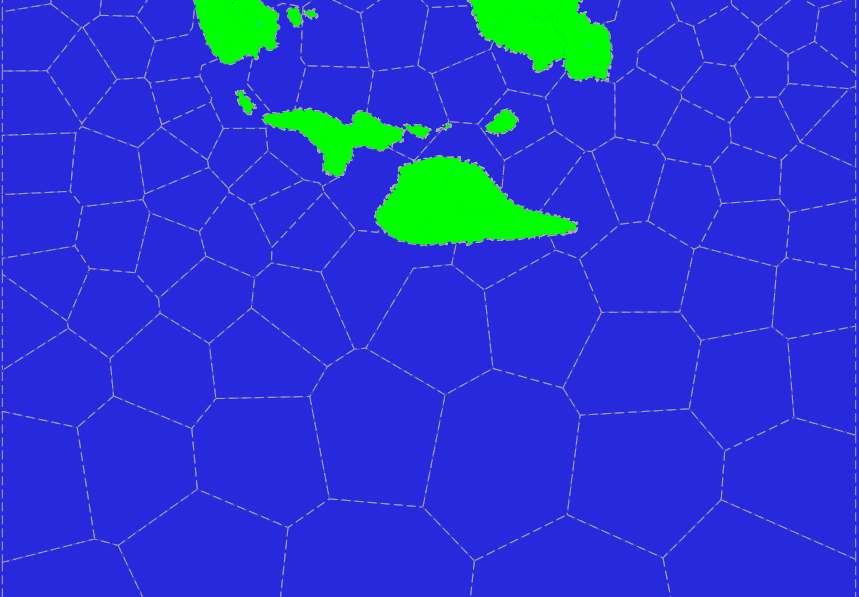
In general, we have achieved what you want from the ocean sectors. Their area is about the same (on the sphere), and they are either convex, or with slight deviations from the convexity.

The main function for the generation of ocean sectors:

 map.makeOceanSectors( world Geometry, avg_vp_areaKM Double Precision, merging_ratio Double Precision, merging_method Int ) RETURNS Void 

world - "world" polygon, which serves as the borders of the world.
avg_vp_areaKM - the average area (km ² ) of the polygons from which ocean sectors are made.
merging_ratio - share avg_vp_areaKM , such that if the area of ​​the sector is less than it, then it will be attached to the next.
merging_method is a merge method ('1' or '2').

Example. We build sectors in a given "world" polygon with an average area of ​​basic polygons of 1,000,000 km ² . Sectors whose area will be smaller than half of this value will be added to the others. The second merge method is used - by the nearest center.

 SELECT * FROM map.makeOceanSectors( ST_GeomFromText( 'POLYGON((-75 -85, 75 -85, 75 85, -75 85, -75 -85))', 4326 ), 1000000, 0.5, 2 ); 

Segments of continents.

On the continents, you can enter a more interesting division, based, on the one hand, on a set of small basic polygons, and on the other, on natural objects, such as rivers and watersheds. The structure thus obtained is very similar to the map of states and provinces in them. That is, this is a process of procedural generation of a political map of the world .

Unlike the segments of the oceans, the bulge becomes completely optional.

There are no watersheds on forgedmaps.com yet, but there are already rivers. Using rivers in a script requires them to be presented in MultiLineString . They have such an idea in the riversz file . When importing into the database, you can immediately get rid of the z-coordinates that are unnecessary in this process. Other required data, namely, the boundaries of land, are in the shapefile of the lands . Each land area has an identifier aid (area Id) and may consist of a continent and the nearest islands or only of small islands located closely.

For our example, we choose the average sector size of 40000 km ² and the average size of the base polygon of 5000 km ² . This is a fairly large size, chosen so just for clarity. Smaller sizes are also acceptable (up to the read m ² ), but watch the computation time and use the appropriate database configuration.

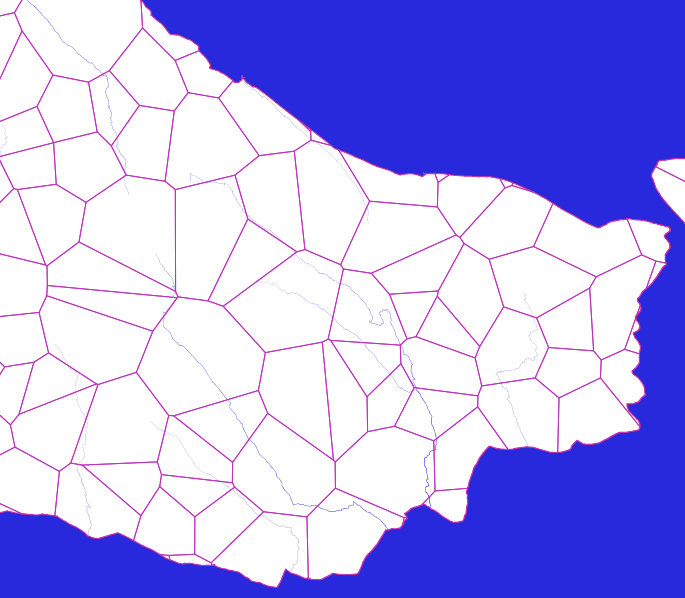
This picture is an example of how the base polygons look inside the land area.



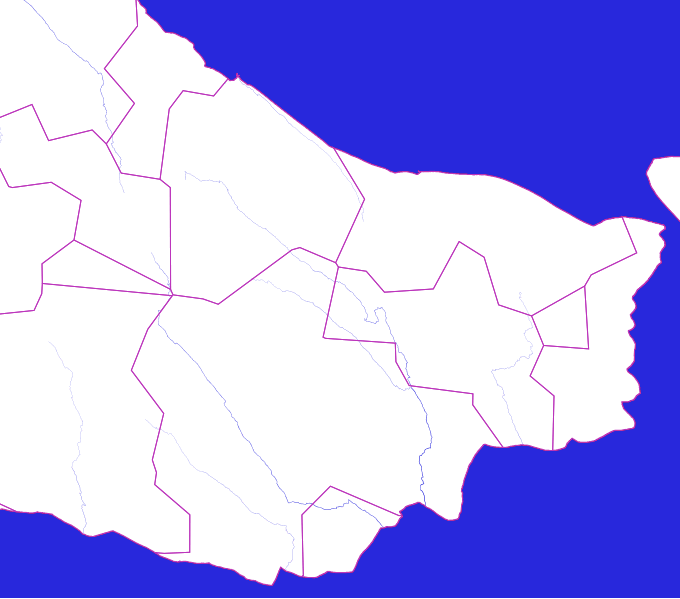
The next step is to make the integration of base polygons into sectors. To do this, we randomly select from the base polygons as much as we want to make sectors and gradually connect adjacent polygons to the accumulating sectors.



Now it is time to take into account the river. We use them to divide sectors into
separate parts by the ST_Split function. Such a division can be performed depending on certain conditions: the final flow of the river or the area of ​​the part to be separated.

Now we can see how some borders go along rivers.



We attach small parts of sectors to large sectors. But at the same time we must try
do not attach parts to the same sectors from which they were cut off.



We have managed large areas of land, but small islands still remain. Those of them that have an area close to the average area of ​​a sector are made into separate sectors immediately. But with those whose area is much smaller than the average sector, we act in two ways.

1. If such islands are located relatively far from already existing sectors, then we make them separate sectors. “Far away” here depends on a given average area of ​​the sector: the smaller this area is, the more likely it is that the island will become a separate sector.

2. If the island is close to other already established sectors, then it is combined with one of them. Namely, with the one that has the largest area in some landfill obtained using ST_Buffer from this island.



Here, four islands fell into two different sectors. If you increase the specified average area of ​​the sector, then sooner or later all the islands will fall into one single sector.

The main function for generating sectors on land:

 map.makeLandSectors( aid BigInt, avg_vp_areaKM Double Precision, avg_sector_areaKM Double Precision, max_sector_cut_area_ratio Float, pref_min_island_area_ratio Float, min_streamflow Int ) RETURNS Void 

aid is the identifier of the land area.
avg_vp_areaKM - the average area (km ² ) of the base polygons.
avg_sector_areaKM - average area (km ² ) of sectors.
max_sector_cut_area_ratio - share avg_sector_areaKM , which defines the maximum area that can be cut off by the river.
pref_min_island_area_ratio - share avg_sector_areaKM , which determines the minimum area, with which the island immediately becomes a separate sector.
streamflow - if a river has a final flow not less than this value, then it participates in the cutting of sectors.

In the following example, using the function will create sectors on a plot of land with aid = 5. The base polygons with an average area of ​​5,000 km ² will be used to create sectors with an average area of ​​40,000 km ² . Also, at the same time, the maximum area cut off by the rivers will be 0.125 * 40000 km ² , and 0.25 * 40000 km ² is the minimum area at which the islands immediately become sectors. For cutting sectors by rivers, rivers with a minimum final runoff are used 2.

 SELECT * FROM map.makeLandSectors(5, 5000, 40000, 0.125, 0.25, 2); 

Links

An SQL script code is available that does all the work, including creating sectors and building transition graphs between adjacent sectors. GIS data procedurally-generated planets can be taken from forgedmaps.com . You can use the GIS data of the Earth , bringing them to a similar structure. You can also, using any modern GIS , make data manually from scratch or get new data by converting data obtained from any other source. More complete instructions for the script can be found in the manual .