Introduction

This brief article will tell you how the model of atmospheric light scattering is arranged in our latest 4k Intra Appear by Jetlag , the party version of which took the honorable 12th place in 4k intro compo on the Revision 2018 demopati in April of this year.

Download the binary for free without SMS here .

If, however, you don’t have Windows, or you don’t have a powerful modern video card, then there’s a consolation card:

The music for this work was written by keen using 4klang . All the code and visuals remained behind me.

Only the light scattering model will be discussed here. Other things, such as: tools, model of the city, model of lighting and materials, are not affected. I can send the brave ones to read the source code , or watch the recording of how I’m drowning for hours - most of the development got on the video.

A boring story you can skip

The work on this work began with the realization that the main full-working-day work leaves no time to work on a full-fledged 4k job - it is almost mid-March in the yard, a couple of weeks remain before Revision.
It remains only to come up with something simple enough for a quick, for a couple of evenings, a comp-filler. Doing another stupid reymarch is not respecting the viewer, so I remembered that a few years ago I had to do a shader with scattering, and it was quite simple, compact and at the same time admissible beautiful, although rather slow.

In the course of a brief discussion, I insisted on my own, and we decided to dwell on the following: to make the landscape flooded with diffused light, with sunset, clouds and twilight rays (TIL as translated as "god rays"). In order not to lift up the number of steps in the atmosphere to completely non-interactive values, it will be necessary to rake strongly with rays (a yard Monte Carlo method), which will generate visible noise. But it does not matter if the camera is moved and the scene is changed slowly and the ambient track is started, then you can mix the neighboring frames painlessly and temporarily smooth this noise.

Keen wrote the music pretty quickly - she was almost ready two weeks before Revision. However, I was seriously undermined by the flu - with an ambulance and an infectious disease - so I practically did not start working on the shader until the moment when I got on a plane to Frankfurt, more or less somehow alive. The prototype of this scattering model was written in the air.

We already quickly collected the party-version of the intro from sand and drool at the party itself for several hours left before the deadline (and, probably, a couple - after; D), while I was away from the flu, lack of sleep, hours-long flights, and I was constantly distracted by participation in the Shader showdown livecoding compo .

The version shown on the big screen contained a lot of artifacts and only the rudimentary geometry of the city based on the Voronoi diagram with random heights.

In general, 12th place is quite generous.

The final version shown above was made later and in a more relaxed mode, 1-2 evenings a week for a month. In total, the work took about 40-50 hours of work.

Scatter model

(Note: I do not do graphics programming professionally. This is my little cozy hobby for good, if a hundred or two are very defocused under beer wine hours a year. Therefore, there is no chance that some things below are described and / or named incorrectly. Uncle, beat!)

The scattering model was borrowed from Comrade Egor Yusov ’s article "High Performance Outdoor Light Scattering Using Epipolar Sampling" , published in GPU Pro 5 , with a fully ejected epipolar sampling.

Physical model

Sun photons bombard the atmosphere of the earth and interact with air particles. A photon can be scattered by a particle, which entails a change in the direction of the photon, or it can be absorbed, which means that the photon is lost, and its energy has been transformed into some other form.
Both processes are probabilistic and depend in particular on the particle density and photon energy (which corresponds to its color).

On the fingers, "red" photons have a lower probability of interaction with the air, so they overcome the thickness of the atmosphere relatively intact.
“Blue”, however, have a higher probability of dispersion, which is why they can change direction repeatedly and travel considerable distances in the atmosphere before reaching (or not) the observer.

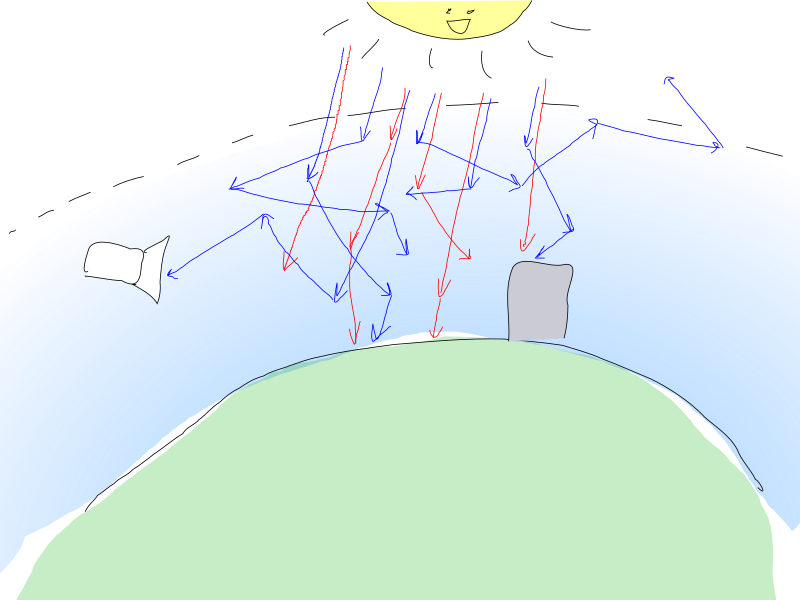
The parameters of interaction of light with air that we are interested in are as follows:

• $$$\ beta ^ s (x)$- the proportion of scattered light per unit length at a point $$$x$
• $$$\ beta ^ a (x)$- proportion of light absorbed per unit length at a point $$$x$
• $$$\ beta ^ e (x) = \ beta ^ s (x) + \ beta ^ a (x)$- total fraction of the lost light per unit length at the point $$$x$
• $$$p (\ alpha)$- the angular distribution of the scattered light, where $$$\ alpha$this is the angle between the incident and scattered rays

It is assumed that air consists of two types of particles, the scattering on which occurs independently: molecules (Rayleigh model) and aerosols (relatively large spherical particles, Mie scattering in the English-language literature). Models differ only in different values ​​for the parameters above.

For both models, it is assumed that the density of the corresponding particles decreases exponentially with height: $$$\ rho = \ rho_0e ^ {- \ frac {h} {H}}$where $$$\ rho_0$- density at sea level. Coefficients $$$\ beta$proportional $$$\ rho$and their values ​​below are given for sea level.

Rayleigh model

• $$$p_R (\ alpha) = \ frac {3} {16 \ pi} (1+ \ cos ^ 2 (\ alpha))$[Nishita et al. 93, Preetham et al. 99]
• $$$\ beta_R ^ a = 0$
• $$$\ mathbf {\ beta_R ^ e} = \ mathbf {\ beta_R ^ s} = (5.8, 13.5, 33.1) _ {rgb} 10 ^ {- 6} m ^ {- 1}$[Riley et al. 04, Bruneton and Neyret 08]
• $$$H_R = 7994m$[Nishita et al. 93]

Aerosols

• $$$p_M (\ alpha) = \ frac {1} {4 \ pi} \ frac {3 (1-g ^ 2)} {2 (2 + g ^ 2)} \ frac {1+ \ cos ^ 2 (\ alpha)} {(1 + g ^ 2 - 2g \ cos (\ alpha)) ^ \ frac {3} {2}}$[Nisita et al. 93, Riley et al. 04] where $$$g = 0.76$[Bruneton and Neyret 08]
• $$$\ beta_M ^ s = 2 \ cdot10 ^ {- 5} m ^ {- 1}$[Bruneton and Neyret 08]
• $$$\ beta_M ^ e = 1.1 \ beta_M ^ s$
• $$$H_M = 1200m$[Nishita et al. 93]

Single scatter approximation

The scattering approximation is based on the transmission of a beam from each pixel of the camera and calculating how much light from the atmosphere should come from this direction. All three RGB components of light correspond to each beam, as if three photons with corresponding energies fly along this beam.

The light reaching the chamber is formed by the following processes in the air:

• Scattering (TIL, that FIG know how in-scattering is translated). Light emitted by the sun is added, which is scattered in a probabilistic manner at an angle corresponding to the direction of the camera.
• Absorption . Light already flying along the beam is absorbed by the air.
• Scattering Light already flying along the beam is lost by scattering in other directions.

For performance reasons, we believe that the light from the scattering can get in the direction of the camera only once, and the rest of the light (which was scattered more than once) can be neglected. This is not recommended for twilight, but what to do.

This approach is depicted in the following beautiful image (I tried!):

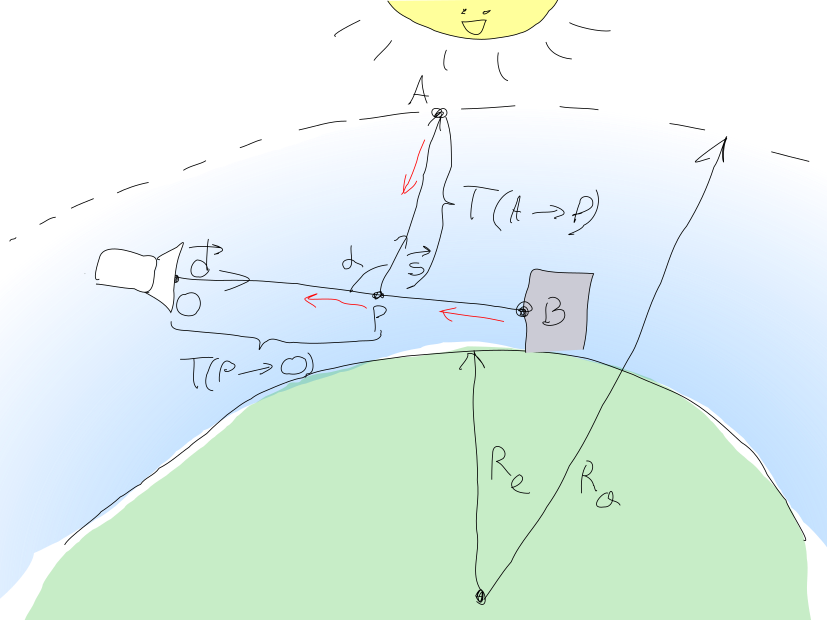
Thus, the amount of light that must be detected by a camera pixel at $$$O$can be calculated as an amount $$$\ mathbf {L} = \ mathbf {L_ {in}} + \ mathbf {L_ {BO}}$where $$$\ mathbf {L_ {in}}$- scattered from the sun, and $$$\ mathbf {L_ {BO}}$- the amount of light from a point $$$B$the object geometry of the scene reaching $$$O$.

Light geometry

$$$\ mathbf {L_ {BO}} = \ mathbf {L_O} e ^ {- \ mathbf {T} (B \ rightarrow O)}$where $$$\ mathbf {L_O}$- it is light emitted from a point $$$B$in the direction of the camera.

$$$\ mathbf {T} (B \ rightarrow O)$called the optical thickness of the medium between the points $$$B$and $$$O$, and is calculated as follows:

$$

$$\ mathbf {T} (B \ rightarrow O) = \ int_B ^ O (\ beta_M ^ e (s) + \ mathbf {\ beta_R ^ e} (s)) ds$$

Whereas members are $$$\ beta$consist of a sea level constant and variable density, this expression can be converted to:

$$

$$\ mathbf {T} (B \ rightarrow O) = \ beta_M ^ e \ cdot \ int_B ^ O \ rho_M (s) ds + \ mathbf {\ beta_R ^ e} \ int_B ^ O \ rho_R (s) ds = \ bar {\ mathbf {\ beta}} \ cdot \ bar {T_ \ rho} (B \ rightarrow O)$$

Please note that I do not specifically disclose $$$\ rho$, because we will change them further when adding clouds. Also pay attention to the fact that $$$\ beta$- RGB vectors (at least $$$\ mathbf {\ beta_R}$have different meanings for the RGB component, and $$$\ beta_M$- vector is just for consistency). Members with $$$\ rho$under the integral - scalars.

sunlight

sunlight $$$\ mathbf {L_ {in}}$calculated by integrating over all points $$$P$along the segment $$$OB$and the accumulation of all incoming sunlight scattering towards the camera and fading away $$$\ mathbf {T} (P \ rightarrow O)$.

The amount of sunlight reaching the point $$$P$calculated by a similar formula $$$\ mathbf {L_P} = \ mathbf {L_ {sun}} e ^ {- T (A \ rightarrow P)}$where $$$\ mathbf {L_ {sun}}$- the brightness of the sun, and $$$A$- the point at which the beam from the point $$$P$in the direction of the sun $$$\ vec {s}$leaves the atmosphere. The proportion of this light that will be scattered towards the camera is $$$\ mathbf {L_P} \ cdot (\ mathbf {\ beta_R ^ s} (s) p_R (\ alpha) + \ beta_M ^ s (s) p_M (\ alpha))$.

Total we get:

$$

$$\ mathbf {L_ {in}} = \ int_B ^ O \ mathbf {L_P} (s) \ cdot (\ beta_M ^ s (s) p_M (\ alpha) + \ mathbf {\ beta_R ^ s} (s) p_R (\ alpha)) \ cdot e ^ {- \ mathbf {T} (P (s) \ rightarrow O)} ds$$

You may notice that:

• $$$\ alpha$is a constant for each pixel-ray of the camera (we assume that the sun is infinitely far and the rays from it are parallel)
• Coefficients $$$\ beta$consist of sea level constants and density functions $$$\ rho (s)$
• Functions $$$p (\ alpha)$have common factors for both scattering processes

This allows the expression to be converted to:

$$

$$\ mathbf {L_ {in}} = \ mathbf {L_ {sun}} (1+ \ cos ^ 2 (\ alpha)) (\ frac {\ frac {1} {4 \ pi} \ frac {3 (1 -g ^ 2)} {2 (2 + g ^ 2)}} {(1 + g ^ 2 - 2g \ cos (\ alpha)) ^ \ frac {3} {2}} \ beta_M ^ s \ cdot \ mathbf {I_M} + \ frac {3} {16 \ pi} \ mathbf {\ beta_R ^ s} \ cdot \ mathbf {I_R})$$

Where

$$

$$\ mathbf {I_M} = \ int_B ^ O \ rho_M (s) e ^ {- \ mathbf {T} (A \ rightarrow P (s)) - \ mathbf {T} (P (s) \ rightarrow O)} ds$$

$$

$$\ mathbf {I_R} = \ int_B ^ O \ rho_R (s) e ^ {- \ mathbf {T} (A \ rightarrow P (s)) - \ mathbf {T} (P (s) \ rightarrow O)} ds$$

$$$I_M$and $$$I_R$differ only in density functions, their exponents are the same.

No one has ever managed to calculate these integrals analytically, so you have to count them numerically, using raymarching (as stated in the original publications, you cannot do it!).

Numerical integration

For reasons of size and laziness, we will be considered as stupid as possible: $$$\ int_A ^ B f (x) dx \ approx \ frac {\ left | B - A \ right |} {N} \ sum_ {i = 0} ^ N f (A + i \ cdot \ frac {\ vec { B - A}} {N})$

The beam will be marched in the direction opposite to the light flow: from the camera point $$$O$before crossing the beam with the geometry $$$B$. Section $$$O \ rightarrow B$divided by $$$N$steps.

Before starting the march, initialize the variables:

• vec2 (two separate components, for Rayleigh and aerosol scattering) total accumulated optical thickness $$$\ mathbf {T_ \ rho} (P (s) \ rightarrow O)$
• vec3 ( vec3 ) $$$\ mathbf {I_M}$, $$$\ mathbf {I_R}$

Next for the point $$$P_i$each step between $$$O$and $$$B$:

1. Let the beam out $$$\ vec {s}$in the direction of the sun and get a point $$$A_i$the output of this ray from the atmosphere.
2. Calculate the thickness $$$\ mathbf {T} (A \ rightarrow P_i)$by first calculating $$$\ int_A ^ {P_i} \ rho_M (s) ds$and $$$\ int_A ^ {P_i} \ rho_R (s) ds$using the same raymarching (with the number of steps M ), and then multiply the resulting terms with the corresponding constants $$$\ beta_M ^ e$and $$$\ mathbf {\ beta_R ^ e}$.
3. Calculate the thickness $$$\ mathbf {T_ \ rho} (P_i \ rightarrow O) = \ mathbf {T_ \ rho} (P_ {i-1} \ rightarrow O) + \ rho_i (s) \ cdot ds$
4. We accumulate $$$\ mathbf {I_R}$and $$$\ mathbf {I_M}$using these values

The final color after raymarching is calculated by the sum of the items:

1. Term $$$\ mathbf {L_ {BO}}$get trivial: a variable containing $$$\ mathbf {T_ \ rho} (P_i \ rightarrow O)$contains value $$$\ mathbf {T_ \ rho} (B \ rightarrow O)$, insofar as $$$P_i$reached $$$B$.
2. Multiply $$$\ mathbf {I_R}$and $$$\ mathbf {I_M}$on the corresponding constants and adding the result is calculated $$$\ mathbf {L_ {in}}$

Shaders

Simple scattering without anybody

A little combed and commented source codes of scattering, taken (almost) directly from the intro itself:

 const float R0 = 6360e3; //    const float Ra = 6380e3; //     const vec3 bR = vec3(58e-7, 135e-7, 331e-7); //    const vec3 bMs = vec3(2e-5); //    const vec3 bMe = bMs * 1.1; const float I = 10.; //   const vec3 C = vec3(0., -R0, 0.); //   ,  (0, 0, 0)    //   //  vec2(rho_rayleigh, rho_mie) vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); //    return vec2(exp(-h/8e3), exp(-h/12e2)); } //    ,        float escape(vec3 p, vec3 d, float R) { vec3 v = p - C; float b = dot(v, d); float det = b * b - dot(v, v) + R*R; if (det < 0.) return -1.; det = sqrt(det); float t1 = -b - det, t2 = -b + det; return (t1 >= 0.) ? t1 : t2; } //         `L`   `p`   `d` //   `steps`  //  vec2(depth_int_rayleigh, depth_int_mie) vec2 scatterDepthInt(vec3 o, vec3 d, float L, float steps) { vec2 depthRMs = vec2(0.); L /= steps; d *= L; for (float i = 0.; i < steps; ++i) depthRMs += densitiesRM(o + d * i); return depthRMs * L; } //   (  --   ) vec2 totalDepthRM; vec3 I_R, I_M; //    vec3 sundir; //    ,    `-d`   `L`   `o`   `d`. // `steps` --    void scatterIn(vec3 o, vec3 d, float L, float steps) { L /= steps; d *= L; //   O  B for (float i = 0.; i < steps; ++i) { // P_i vec3 p = o + d * i; vec2 dRM = densitiesRM(p) * L; //  T(P_i -> O) totalDepthRM += dRM; //     T(P_i ->O) + T(A -> P_i) // scatterDepthInt()    T(A -> P_i) vec2 depthRMsum = totalDepthRM + scatterDepthInt(p, sundir, escape(p, sundir, Ra), 4.); vec3 A = exp(-bR * depthRMsum.x - bMe * depthRMsum.y); I_R += A * dRM.x; I_M += A * dRM.y; } } //    // O = o --   // B = o + d * L --   // Lo --     B vec3 scatter(vec3 o, vec3 d, float L, vec3 Lo) { totalDepthRM = vec2(0.); I_R = I_M = vec3(0.); //  T(P -> O) and I_M and I_R scatterIn(o, d, L, 16.); // mu = cos(alpha) float mu = dot(d, sundir); //     return Lo * exp(-bR * totalDepthRM.x - bMe * totalDepthRM.y) //   + I * (1. + mu * mu) * ( I_R * bR * .0597 + I_M * bMs * .0196 / pow(1.58 - 1.52 * mu, 1.5)); } 

Zaykat shader

Clouds

Not bad, but such a picture could also be obtained much easier by some tricky heap of gradients.

By deceiving the way to get clouds and god rays is much more difficult. Let's add.

The idea is to approximate clouds with aerosols and modify only the densitiesRM() density function. This may not be as physically correct as we would like (I have no idea how scattering of light in the clouds in computer graphics actually approaches).

 //      const float low = 1e3, hi = 25e2; // vec4 noise24(vec2 v) --       // float t --  float noise31(vec3 v) { return (noise24(v.xz).x + noise24(v.yx).y) * .5; } vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); vec2 retRM = vec2(exp(-h/8e3), exp(-h/12e2) * 8.); //    () if (low < h && h < hi) { vec3 v = 15e-4 * (p + t * vec3(-90., 0., 80.)); //    <s></s>      :     retRM.y += 250. * step(vz, 38.) * smoothstep(low, low + 1e2, h) * smoothstep(hi, hi - 1e3, h) * smoothstep(.5, .55, //  :   .75 * noise31(v) + .125 * noise31(v*4. + t) + .0625 * noise31(v*9.) + .0625 * noise31(v*17.)-.1 ); } return retRM; } 

Contrary to expectations, we receive not beautiful clouds, a sweet victory and fans, but artifacts. Attempting to raise the number of steps in the forehead does not completely remove the artifacts, but significantly spoils performance.

Solutions crutches with which the intra is sticking

• The most unpleasant artifacts on the horizon are hiding around the corner.
• Clouds are added only near the camera.
• Monte-Karlovshchina is added, each marched beam is shifted by a random offset: for (float i = pixel_random.w; i < steps; ++i) . This adds the same noise that has to be temporally smoothed by mixing successive frames.

• The number of steps increases for zones requiring more details (for example, a cloud layer). That is why this ridiculous division of functions into scatterImpl() and scatterDepthInt() :

  
  

   //    scatterIn() vec2 depthRMsum = totalDepthRM; float l = max(0., escape(p, sundir, R0 + hi)); if (l > 0.) //   16  depthRMsum += scatterDepthInt(p, sundir, l, 16.); //     4- depthRMsum += scatterDepthInt(p + sundir * l, sundir, escape(p, sundir, Ra), 4.); 

  
  

   //   scatter() //  10    float l = 10e3; if (L < l) scatterIn(o, d, L, 16.); else { scatterIn(o, d, l, 32.); // 8  --     scatterIn(o+d*l, d, Ll, 8.); } 

  
  

Combination with scene geometry

As a result of the traditional re-marking of the distance and shading functions, the distance L to the point B and the color of the pixel Lo already obtained. These values ​​are simply substituted into the scatter() function. If the beam does not rest on the geometry and leaves the scene, then the color Lo zero, and L calculated using escape() - it is considered that the beam left the atmosphere.

Look like that's it.

... Actually, of course, not everything. Quite a lot of pain now grind all the parts to each other so that it generally looks believable. Just a bunch of messing with the twisting of parameters, scene geometry, noise functions, the trajectory and camera angle. I'm afraid I have no good advice here, except for recommending you to iterate for many hours and beat your head against the wall.

Minification

After processing the shader minifier , the final shader scatter code is about 1500 bytes in size. Crinkler compresses it to ~ 700 bytes, which is about 30% of the total shader code.

Removal

I do not know how to computer graphics.