Hierarchical key generation

In this article we will talk about deterministic wallets, hierarchical key generation, as well as how it works mathematically and in which cases it is convenient to use in practice. This material will be useful to specialists whose activities are related to payment gateways, Bitcoin wallets and other coin depositories. In addition, the material will be of interest to those who are interested in elliptical cryptography and electronic signature key deployment schemes.

Deterministic wallet

First, let's define what a deterministic wallet is. When we talk about key generation, we often use the word “wallet”, because in the context of cryptocurrency, owning a private key is proof of possession of coins, and in this case the wallet and key have a similar meaning.

Deterministic wallet is a wallet in which all used private keys were generated from one secret shared by all keys. The peculiarity is that it is possible from one secret to generate as many pairs of keys for an electronic signature as you like. You can use new addresses for each incoming payment and change.

Conveniently, the keys of such a wallet can be easily transferred to another device, backed up and then restored, because in fact you only need to back up one main secret. In addition, all private keys generated from the main secret are not related to each other. It is impossible to trace the connection between the generated addresses (to determine that they all belong to the same user), and having a generated private key, you cannot restore the shared secret.

Main Secret Encoding

Now let's talk about coding the main secret. There is some standardized approach here that was defined in BIP39. This is the so-called Check Encoding encoding the main secret into a mnemonic phrase - a set of words that is easy to write down on paper and remember if necessary. When entering, it is possible to check the checksum, that is, to identify an error, if any, with a fairly high probability.



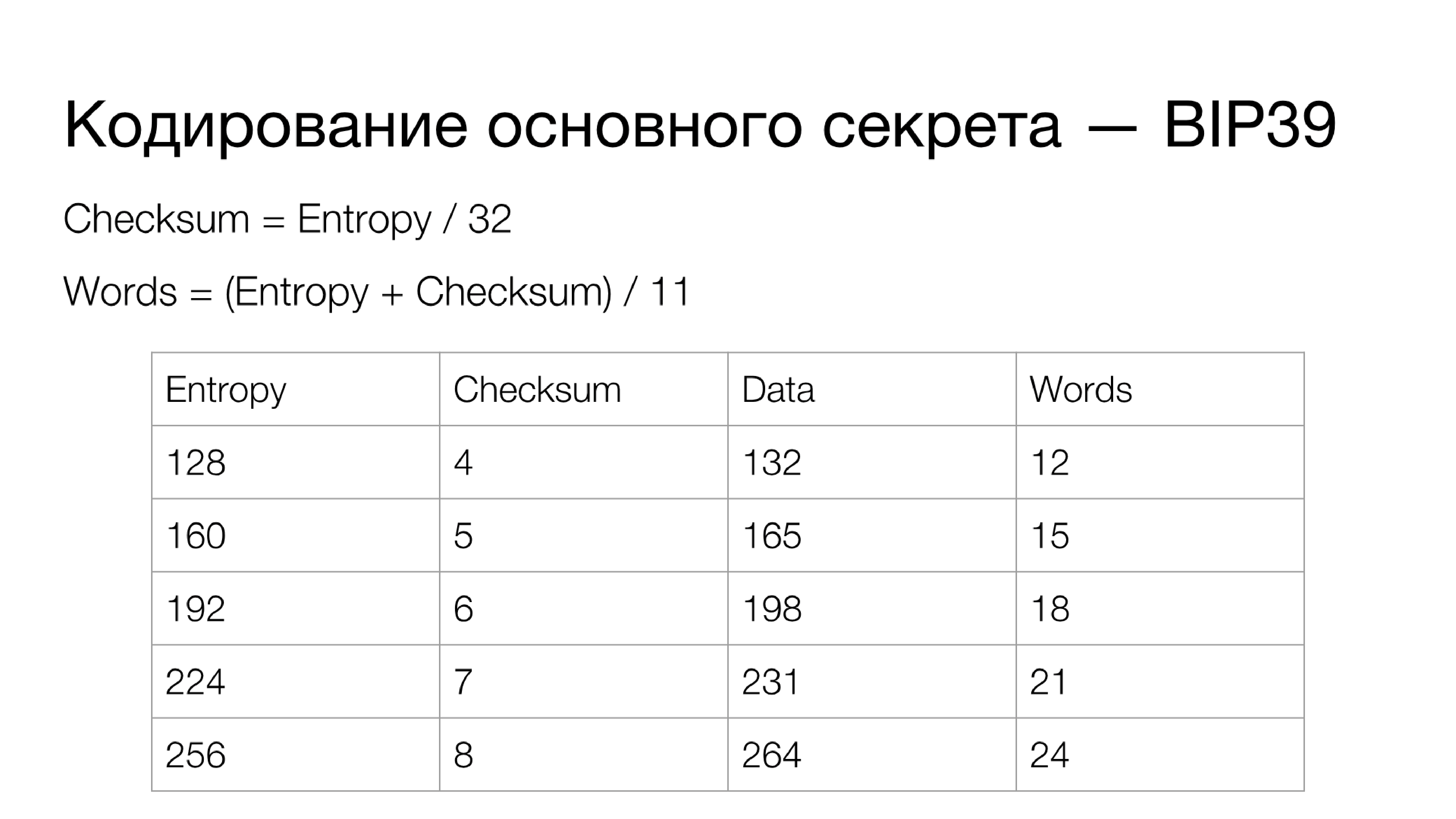
How it works? In fact, you have the main secret (Entropy) - the data from which all personal keys of the wallet are deployed. This secret can be of different lengths. As for the checksum: for every 32 bits of Entropy there is 1 bit of checksum, that is, the Checksum formula is calculated as the length of the Entropy in bits divided by 32.

Entropy is concatenated with a checksum, which is calculated as a double SHA-256 hash (SHA-2 at a length of 256 bits), after which the required number of bits is cut off. The concatenated data is transferred to another number system: from binary to number system on the base of 2048 (as we see, 2048 is $$$2 ^ {11}$ ). And if you add the length of the Entropy bits and the checksum, you get a number that is a multiple of 11. Thus, we get the number of words in the output mnemonic phrase.

In fact, data is “sliced” into 11 bit parts. There is a dictionary consisting of 2048 words ( $$$2 ^ {11}$ ) to which certain requirements are applied. The default language of the dictionary is English, but any can be used. Words must not exceed a certain length (usually a limit of up to 7 characters). All of them must be encoded in UTF-8 with a certain normalization of all characters. Mandatory is the uniqueness of each word on the first four characters.

The first four characters uniquely identify a word in the dictionary, and the remaining characters are used to complete the word to a convenient form for reading, memorizing, etc. Thus, each piece of data consisting of 11 bits gets a one-to-one correspondence in the form of a word from dictionary. If your secret Entropy is 256 bits, then the data to encode will be 264 bits, and your mnemonic phrase will contain 24 words. This is the main approach to coding the secret of the wallets in BIP39, which is used in practice most often.

In order to make a backup copy and use it in the future, you are offered to write this phrase out to external media. Paper that you will keep in a safe place is best suited. So you can restore full access to all your keys.

Types of deterministic wallets

Deterministic wallets are of two types. Consider their main differences.

The first one is the easiest. The main secret here is concatenated with the index of the child key that we want to receive, after which the concatenated data is hashed. Most often this happens using the SHA-256 hash function.

The second type includes hierarchical deterministic wallets (hierarchical deterministic wallets, HD wallets), the principles of which are defined in BIP32, and are a very common approach to hierarchical key generation.

Deterministic generation

Consider the differences between these types of wallets in the diagram.



An ordinary deterministic wallet has a certain seed, from which a huge amount of private keys are directly generated. Their number can only be limited by the index dimension, which is concatenated to a secret before hashing. Usually it is 4 bytes, that is, the space of possible variants allows for about 4 billion unique keys of a deterministic wallet. In practice, this should be enough for any situation.

Hierarchical deterministic generation

Let us turn to a hierarchical deterministic wallet, the key unfolding scheme of which is still presented in a simplified form. There is a seed, from which a pair of master keys is directly obtained. If in a regular deterministic wallet we get a private key, here we get a pair of keys. Moreover, there are levels of hierarchy, on each of which we calculate an index for generating a child key. We can also build public key branches and private key branches.

Hierarchy levels

Regarding HD wallets, it is worth noting that, according to the BIP32 rules, at each level of the hierarchy, the spawning node has three objects: a private key, a public key (public key), and a chain code (chain code) that is used to generate the next level of hierarchy.

Hierarchical generation scheme

Let us consider in more detail the scheme of key generation using BIP32.



It all starts with the seed, it is also called the master seed, from which the zero level of the hierarchy is calculated - a pair of master keys and a chain code.

From a pair of master keys can be generated a huge variety of key pairs with certain indices. Formed a new level of hierarchy, which is used to generate accounts. Suppose one user has a seed and he wants to create several addresses that will be different from each other. Coins of these addresses will not be mixed, will not be published together, and in the ready transactions between them it will be impossible to find a link. These keys will be used completely separately from each other. In one of the accounts, a group of keys will be used for the working budget, in the other - for a personal budget, and another account - for black bookkeeping. Coins will not mix with each other.

The next level of hierarchy defines different key generation chains. Most often, chains with indices 0 and 1 are used. The chain with index 0 will generate the final keys to form the address for incoming payments, and the chain with index 1 will generate wallets to which coins sent by the user to themselves, that is, change, will arrive. It is necessary for the purse at the program level to distinguish payments sent from the outside from delivery, to calculate changes in the balance of each transaction and to make a clear list with a history of all payments. This simplifies the development of the wallet and its use for everyday payments.

Hash-based message authentication code

Now let's move on to the mathematical component of the processes of hierarchical key generation. To begin with, consider the hash-based message authentication code. This is another class of hash functions. It differs in that it takes two values ​​at the input, not just one. The first value is the secret key, and the second is the message itself.

$$

$$HMAC (K, m) = H ((K ^ {opad}) || H (K ^ {ipad}) || m))$$

K - key
m - message
opad, ipad - some constant values ​​needed to form keys that differ from each other at different stages of hashing.
SHA-512 is used as a hash function.

The special feature is that in order to use HMAC, you need to have a secret key in order to get the correct hash value of the message.

So, to calculate the HMAC hash value, the XOR key value is with the constant ipad value, after which the result is hashed. A message is concatenated to this value, after which the XOR key is calculated with a constant value, concatenated with a hash value, and then hashed again. As a result, we get 512 bits of hash values.

Derivation Functions

Let's look at several functions that are used in the calculation of hierarchical keys.



First of all, we are interested in converting the master seed to a master key pair. After that, you need to obtain from the personal parent key a child private key and a child public key. In the second case, the same function is used as in the first, but the multiplication of the number by the base point is added, so it will not be considered separately. The next step is getting the child public from the public parent key. It is worth noting that it is impossible to obtain a child personal from the parent public key. This limitation is due to certain properties inherent in HD wallets, which we will look at next.

So, let's go through each of the generating functions separately.



To obtain the master key from the master-sid, the HMAC function is used, where the constant string “Bitcoin seed” is transmitted as the key, and the message itself is the main secret data. Thus, we have a 512-bit hash value, which we consider as two parts: left and right. The left side is the master private key, and the right side is the chain code. Further, these values ​​will be used to generate subsequent levels of child keys.

In order to get a master public, it is enough to multiply the value of the base point by the value of the master private key. As you can see, this happens by analogy with ordinary keys in a group of points on an elliptic curve.

Now let's see how the child private key comes from the parent private key.



Let's use the HMAC function again. As a key, we pass the chain code of the current hierarchy level, and as a message, concatenation, where the first part is the personal parent key multiplied by the base point. In fact, this is a cast to a point and the serialization of this point. Concatenation occurs with the index of the child key that we want to receive, serialized to 32 bits, that is, to 4 bytes.

According to the result of the HMAC function, we get the value of I, and again we consider it separately: the left and right sides of the output values ​​are 256 bits each. Then a child private key $$$k_i$ we calculate by adding to the left output value $$$I_L$ parent private key values. Addition is performed modulo n, where n is the order of the base point of the elliptic curve, in order not to exceed the maximum value of the private key. So we got a child private key.

Accordingly, the child chain code will be equal to the right output value of the HMAC function, that is, $$$I_R$ . If we want to find a child public key from the private parent key, multiply the value $$$k_i$ on the value of the base point on the elliptic curve. So we get the public key $$$K_i$ .

How do we calculate the child public key from the public parent key?



Here the calculation will be slightly different. We pass the key chain code of the current hierarchy level to the HMAC function, after which we serialize the parent public key and concatenate it with the necessary index serialized into 32 bits. Input data is obtained in exactly the same way as in the previous case. To calculate the public key, we take the left part of the output value of the HMAC function, and consider it as 256 bits, taken modulo the order of the base point, lead to a point on the elliptic curve, that is, multiply by the base point, then add the result to the parent public key . The result of the addition will also be a period, and this will be the public child key. The chain code for this key will be the right side of the output value of the HMAC function.

Matching keys to each other

There may be a logical question about how the private and public keys obtained in different ways will correspond to each other. Is it possible to get exactly the same value from a publicly generated public key by taking a private key obtained in another way and multiplying it by a base point? It is easy to check.



If we recall how we calculated the personal child key, and multiply it by the base point, that is, bring the point function, and then recall the child public key calculation and compare these calculations, we will see that if we consider the parent public key as a product of the personal parent key to the base point, we will see that the same calculations were made, just in a different order.

In one case, we added the private keys and multiplied by the base point, and in the second case, we first multiplied the values ​​by the base point, and then added them together and got the result. Based on the fact that the operation of adding points on an elliptic curve is additive, we can say that these two values ​​are equal - we get the same public key, calculated in two ways.

Sample public key

For fun, we can look at an example of a public key that was obtained for test values ​​and BIP32 calculations. If our Entropy consisted of 128 bits, then in hexadecimal notation it would look like the image below.



The same value, encoded into a mnemonic phrase on BIP39, will look like the 12 words shown. If you use this mnemonic phrase as a master seed for hierarchical key generation, then you will get such a master private key with the corresponding chain code of 256 bits each.

Extended keys

There are also such concepts as an extended public key and an extended private key. How is it used? To better understand, we describe the visual situation.

Suppose we have a specific user and some service. The service with a certain frequency transfers payments, for example in bitcoins, to the user. Both the user and the service are interested in using a new address for each payment in order to make it difficult for an outside observer to establish the fact and confuse the history of interaction with each other.

In the simplest case, it would look like this: for each incoming payment, the user forms a new key pair, calculates the address that is sent to the service, after which the service can form a transaction and make a payment. However, it is inconvenient for any of the parties if the intensity of these payments is high.

Extended public key

In this situation, the extended public key (extended public key, xPubKey) helps to get rid of inconvenience. The user can enable a third-party service to generate such addresses, which will be known to the service, but only the user will have private keys. The service can generate any number of addresses without the user's knowledge and send funds to them, and the user can, when it is convenient for him, expand his private keys and get access to any of these addresses.

How it works? The user needs to generate a new account at the second level of the key hierarchy, calculate for it the public key and the chain code for the current level. After that, you need to transfer to the service both the public key and the chain code. For convenience, Base58Check Encoding coding was introduced, which we talked about (there is a special version here). Further, the public key, chain code and checksum are concatenated. This is all encoded into the base 58 base system and we get the public key already encoded according to a certain standard. It starts with the characters “xpub”, which is easily recognized. It will look as shown in the image.



The service can accept such a key and deploy the public keys for the user via BIP32, get addresses from them and pay for them. However, only the user can calculate the corresponding private keys.

Hardened derivation

In hierarchical key generation there is such a thing as hardened derivation. This is an approach that does not allow child public keys to be calculated from the corresponding parent public key. This differs from the normal generation in that we use the HMAC concatenation of the serialized point as the parent public key as a message of the HMAC function, and in hardened derivation we use the serialization of the parent private key.

In addition, index calculation is different. The index in normal generation is directly serialized to 32 bits, and in the hardened derivation it is somewhat transformed: a constant value is added to it $$$2 ^ {31}$ that sets the most significant bit to 1 (it becomes easy to distinguish the types of derivation). Accordingly, the space of options for possible keys is the same for both normal generation and hardened derivation and $$$2 ^ {31}$ .



Thus, having a parent public key and hardened derivation, it is impossible to calculate the child public keys. If an attacker receives a parent public key, he will not be able to calculate the child keys. Therefore, it will not be able to calculate the addresses and their connection with the obtained parent key. In the case of normal derivation, that is, in the usual, such a function can be used and trace the relationship of addresses among themselves.

Ways of generation

Let's talk about the ways in which keys can be generated.



At each level of the hierarchy there is a specific index that defines aspects of key generation. The path from the Master key to the final key can be written through slashes as indices. If we are talking about a private key, the entry begins with a small “m”, and if we are talking about generating a public key, then with a large “M”. If the index is indicated by an apostrophe, then it should be understood that this is a hardened derivation, without an apostrophe - normal derivation.

Consider one of the popular ways of generating keys, which is used in BIP32, where hierarchical keys were defined.



It uses a path where the master key is the zero level of hierarchy. This is followed by account indexes that denote the same user, followed by chains, where there can be chains of addresses that are published externally for accepting incoming payments, and with index 1 those chains will be created to which the user himself sends payments all this surrender). The final index will be used to generate those keys from which addresses will be calculated.

In order to use the BIP32 standard to calculate the very first key with the index 0, we will have m, 0 with the generation hardened, chain - 0, index - 0 (m / 0 '/ 0/0). So we get the path for the first hierarchically generated key.

There is a suggestion for improving Bitcoin, it is called BIP43, which implies writing to the first level of the improvement number hierarchy, which offers a new generation path (m / bip_number '/ *).



Thus, BIP44 appeared, which used the feature of the previous sentence, that is, an index of 44 is recorded for the first level of the hierarchy, and proposed the following improvements: write a certain value in the index of the second level of the hierarchy that will correspond to the type of coin we use for this wallet. Now, keys for different currencies can be deployed and used in one wallet.



For Bitcoin, the path will look like “m / 44 '/ 0' / 0 '/ 0/0”, for Bitcoin testnet - “m / 44' / 1 '/ 0' / 0/0”, for Litecoin - “m / 44 '/ 2' / 0 '/ 0/0 ”, for Dash -“ m / 44' / 5 '/ 0' / 0/0 ”. Interestingly, Ethereum uses the exact same elliptical curve for calculating keys and digital signatures and for its wallet the path will look like “m / 44 '/ 60' / 0 '/ 0/0”.

There is another improvement - BIP45. The improvement is aimed at determining the rules for generating keys in the case of their use in multisignature wallets and the formation of addresses according to BIP16, that is, P2SH. It includes the BIP43 sentence and indicates index 45 at the first level of the hierarchy; at the second level it requires the indication of a signer (cosigner).



For example, there is a 3-of-5 multi-signature rule. Consequently, there are 5 signatories, but to spend coins, you need at least 3 signatures. Thus, each of the signatories will have an HD wallet with his master sid, and will indicate his own sequence number in his path. It can be calculated as an index when sorting keys generated at the first level of the hierarchy of each user. For example, at the first level, each user has generated keys, they exchange with each other, sort and find out who has the index for the second level of the hierarchy. This is necessary in order to further eliminate the need to interact in a similar way, and immediately generate the addresses correctly and know your order number.

That is, you can exchange the extended public key once, so that you can create multisignature addresses independently and independently of other members of the group and accept payments on them.

Questions

Let us turn to frequently asked questions.

- How do master seeds differ in different coins?

Seed is a randomly generated number, some kind of bit sequence, or is it a mnemonic phrase, generated, for example, by BIP39, which is used to generate keys. It can be used for one coin, as well as for any other - it is not necessary to use different mnemonic phrases for different currencies. Moreover, there is BIP44, which defines the key generation rules for different currencies from the same mnemonic phrase. These private keys will not overlap with each other, but will be used for different addresses of different currencies.

- Dictionary from BIP39, where 2048 words for mnemonic phrase is standardized? Can I use it in all wallets and applications?

The fact is that this standard is described for BIP39. It is for BIP39 that there are dictionaries: English, two Japanese, Chinese, Italian, Russian, Ukrainian, etc. That is, if some application declares that it uses BIP39 and makes it possible to import and export a mnemonic phrase, this means that it uses same However, there are wallets that use not their own BIP39, but their own modification. It is necessary to look at the description of the wallet and use either standardized or its own development, or the development of the service that the wallet offers.

- On the stock exchanges and centralized repositories such as Coinbase, are the keys of all users' wallets generated from one common for all sid-phrases or not?

It is difficult to say, because they do not open their internal structure, but those new services that appear can either generate keys separately, use the BIP32 standard, or use its modified version. Those services that existed even before the standards for hierarchical key generation appeared, most likely, continue to generate just individual private keys. Perhaps it is easier to manage them if there is a large turnover of all keys.

- The key is a point on an elliptic curve, that is, two very large numbers X and Y?

The public key is yes, it is a point on the elliptic curve, and the private key is a natural number that indicates how many times the base point must be added with itself. The public key itself consists of two values ​​- these are the X and Y coordinates, each of which has a size of 256 bits.

- What is “cast to a point” and serialization of a point and an index?

Coercion to a point means that there is a natural number, which we consider as a private key. We add the base point to itself so many times, that is, in the group of points on an elliptic curve, only the addition operation is defined, then we can multiply the point by a natural number. By point serialization is meant to record in a certain way two coordinates. This may be a compressed entry, but not necessarily. Compressed in the sense that one of the coordinates, namely, Y is transformed into a sign, then the data are substituted into the equation and look at where the point is: higher or lower. In the case of serialization of the index you need to understand that the usual number, which, depending on the size, can be written in bytes or bits. The larger the number, the more data will be needed. In the case of the calculations that we considered, a number of a certain length is required. It is necessary to serialize it to a certain length - 4 bytes. As a result, we mean the conversion of the index to a 4-byte number. If the upper values ​​remain empty, then they will be zero.

- Who came up with these calculations for the derivation of HD wallets functions? Why exactly such formulas, where there are justifications and where it is possible to read more about it?

You can read more in BIP32, if you are interested in the mnemonic phrase, then in BIP39, etc. You can open GitHub, find the user under the nickname Bitcoin. It has a Bitcoin repository, where Bitcoin source code is stored, and a BIPs repository (source), where all suggestions for improving Bitcoin are recorded.

It was thought up to do the calculations in this way, because it is tied to a group of points of an elliptic curve. When they wanted to achieve such functionality that allows you to count separately the branches of public and private keys, while maintaining their consistency with each other, it was the easiest way to implement. In fact, the developers used the simplest option, which allows to achieve interesting properties using the cryptography that has been tested by time. There are a lot of authors of the proposed improvements. The Bitcoin community, whose members offer some kind of development of improvements and mathematical transformations, is quite large.

- Hardened derivation is always only at the second level of the hierarchy?

It all depends on the situation. In the case of generating keys for a multi-signature, it makes sense to do hardened derivation only at the first level of the hierarchy. In the BIP44, hardened derivation is applied to the first three levels: the first level contains the number of the BIP itself, the second contains the account number where this is relevant, and the third contains the currency number where this also makes sense. Suppose you are unlikely to like it if you post the public key, and through it, people will be able to track all your addresses in Bitcoin. If you use an account to receive payments from certain services, then you can not disclose this key and hardened derivation you do not need here.

- Where is it possible to apply hierarchical key generation?

You can apply when working with the stock exchange so that the stock exchange always pays you for different addresses. Although in this case it is better to manually organize all this. This is most relevant for digital wallets for everyday use, because here is a very simple process of creating a backup copy of the private keys and restoring the wallet. Generation of keys for different currencies is also supported, and the standard itself is already used in different implementations of digital wallets. It is convenient to transfer keys between such purses using the same mnemonic phrase.

This topic is devoted to one of the lectures of the online blockchain course “ Hierarchical Key Generation ”.