An article with the analysis of the game of a well-known trading network caused a keen interest in
Cloud4Y . Here are short excerpts to get you up to speed:
Once, on a sunny spring morning, while reading the city forum, I came across a link with a simple game from a well-known trading network. The game (action), dedicated to the World Cup, was a simple three-by-three field, filled with soccer balls. By clicking on the ball, we opened the picture with one or another product. When opening three identical pictures, the participant was guaranteed to receive this product for free at one of the chain's stores. Also under one of the balls there was an image of a red card, the opening of which meant the end of the game.
The author of the article began to investigate the reasons for his loss and, as a result of the calculations, he found out the following:
A quick sketch of the formulas on a napkin, and it turned out that the probability of winning is 1/4. For 5 fields we had to tinker, but the calculated probability was also 25%.
...
Running the script, I got an unexpected result - 25% of the winnings. Having played with the number of winning elements and the total number of fields, I found out that the probability of winning in such a game does not depend on the number of fields and is equal to one divided by the number of winning elements increased by one.
We were interested in the correctness of such a calculation and, replacing the napkin with Excel, we set to work in search of mathematical truth. Readers who are interested in the theory of probability, we invite under the cat, in order to verify the correctness of our calculations.
First of all, we find out the rules of the game. In this, the user Habra
Stecenko helped us, without knowing it, in his
commentary . He also writes:
If you look at the author's script, it is written from the assumption that there are MANDATORY on the field three cards of the same product, one more card for five other products, and one red card, while this absolutely does not follow from the game description - the rules do not say that a winning combination must be present on the field.
In the rules, however, it says that only 26 goods are involved. It turns out that the issuance of 9 cards is generated: 8 cards are combinations of 26 products with repetitions, and one card is red.
Under such conditions, the calculation of the mathematical probability of winning is somewhat more complicated than the author of the original post suggested. The game consists of several layers:- The probability to open N cards without opening the red one is the probability of a different game duration, regardless of whether there will be a prize.
- Chance to collect a combination of 3 cards with the same goods. This probability varies with different duration of the game. It is important to understand that a set of 8 cards with goods and always one red one does not necessarily contain at least one pair of identical cards, not to mention three at once.
Let's start with a simple one - with an understanding of how the number of participants will decrease with an increase in the number of cards they open due to the red card rule.
Chances of different duration of the game
We calculate how likely it is that in N tests (open cards) a red one will be opened.UPD: Initially, we calculated the probability of discovering red using a binomial distribution. This did not guarantee us strictly one red card, with this distribution most likely there was one red card, but there could be both 0 and all 9 with a very, very small probability. Again, thanks to Stecenko for pointing out the mistake in the commentary and proposing the right solution .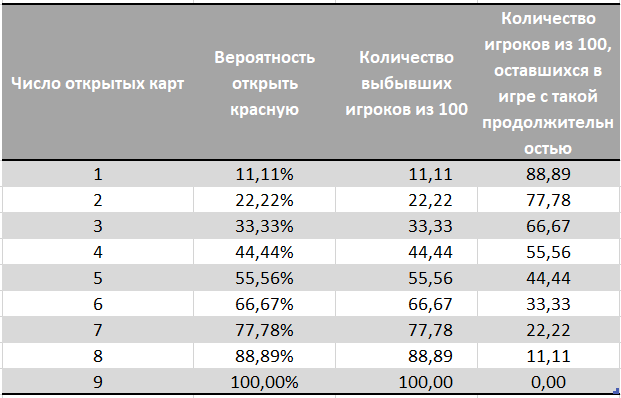
The last column shows how many players from one hundred remain in the game for such a duration. The remaining players are eliminated due to the red card, without knowing whether the winning combination was in the issued set of cards.
Now let's calculate the probabilities of collecting a combination of three cards with the same goods. This is a condition for receiving a prize.
Chances for prizes
We decompose the game logically. We open the first map, and then select a pair for this card, select a triple for a pair. With this approach, we can calculate the probability of getting 3 identical cards in three or more attempts, assuming that all the goods in the game are 26.
For problems with a fixed number of tests or tests, if the outcome of any test can only be success or failure, the tests are independent, and the probability of success remains constant throughout the experiment, we use the Bernoulli formula — in Excel, the BINOM.DIST function.
Using the BINOM.DIST function, it is possible to calculate, for example, the probability that two of the next three newborns will be boys. What is the probability to open three identical ones in three attempts?
= BINOM.DIST (3; 3; 1/26; 0) by mask
= BINOM.DIST (number_s; number_s of tests; probability_s of success; integral)
Or here's a formula for calculating the probability of getting 3
identical and certain goods in 8 attempts.
= BINOM.DIST (3; 8; 1/26; 0), right?
Not really. When we reached the duration of the game in 4 tests, not allowing the opening of red and continuing to play, we get a situation with the possibility of two pairs for the selection of a winning three.
Conventionally, two of the 26 goods are A and B. Our open cards are ABC AB. The probability is no longer 1/26, but 1/26
+ (1/26) * "The probability of two pairs for a given duration of the game .
"The probability of two pairs for a given duration of the game = BINOM. DIST (2; 5; 1/26; 0) ^ 2
When reaching a greater length of the game to the 7th attempt, we have combinations of the type A-B-A-B-B-B. This means that the probability is now equal to
= 1/26 * (1 + BINOM.DIST (2; 7; 1/26; 0) ^ 2 + BINOM.DIST (2; 7; 1/26; 0) ^ 3) and we are looking for a third card for 1, 2 or three pairs.
UPD: Also, initially we did not take into account that the first attempt in our calculation of the gain, cleared of the probability to choose red, is the discovery of any of the 26 goods, which means 100% success. The number of product repeats in the matrix is the number of matches with any one product, which means two repetitions to one product are enough to win, and not 3 matches with a certain conceived result. Thus, the first choice of any card and two attempts to pick up two more of the same form in total three experiments.Knowing the probabilities, we build the matrix:
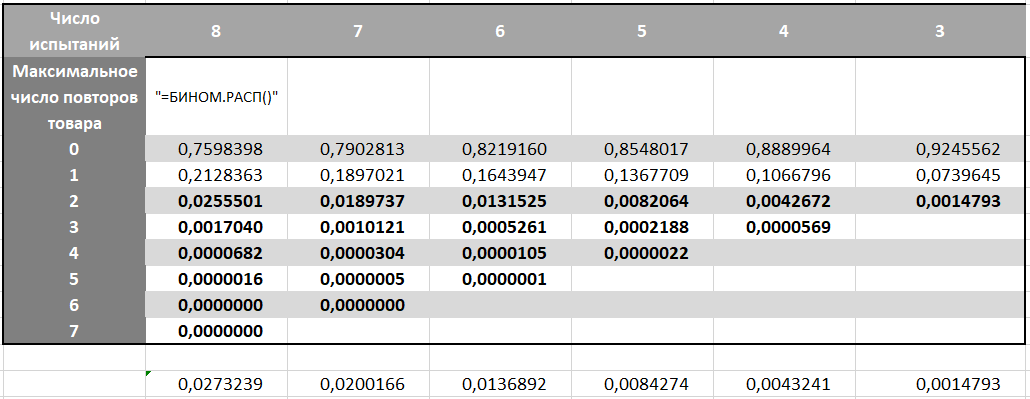
In it we find the probability of each maximum number of repetitions of any product for each variant of the duration of the game. Remember that the probability of winning changes by 4 attempts and by 7, which means we take this into account in the BINOM.DIST formula
We need options with the maximum number of repetitions of any product 3 or more. As the game ends, as soon as we put together the top three, we add probabilities to the columns in the area in bold.
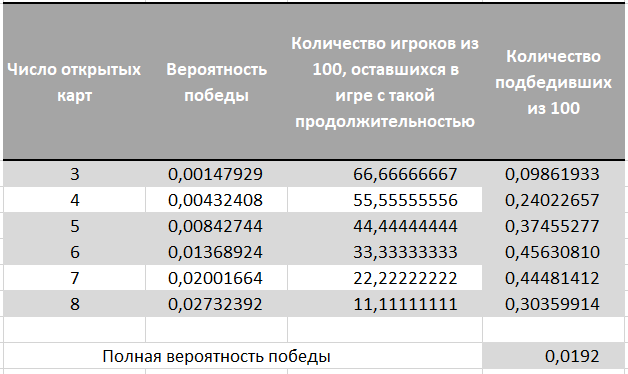
Next, we multiply the odds of each game duration by the chances of winning a prize for such a duration. Summing up these pieces, we get a probability of 0.0192 or 192 winners per 10,000 players.
Yes, indeed it is a very low probability. Not at all 25%. Turn again to the rules of the game:
8. Prize pool:
8.1. Available prizes: names and quantities
...
Total 166,000
We divide 116,000 by the probability of winning and get about 6 million participants in order to play all the prizes. Recall that on January 1, 2018, according to the Rosstat, there were 146,938,921 permanent residents in Russia. Apparently, this is the idea of the organizers of the game - to give a chance to win almost every citizen of Russia.UPD: The final probability has changed after the edits. Now we can test our calculations in practice with the help of scripts, but God's divine gift of the mind of mathematicians-theorists of previous generations, who counted so many probabilities, is amazing, finding the right solution on paper and using mental experiments.The analysis of the code showed the author of the original publication that the script “knows” its result even before the start of the game, but no one knows which predetermined result will give the script to a specific user. Knowing the mathematical side of the issue, you can make a conclusion about the honesty of the organizers.