Translator's Introduction to Clustering Algorithms .Take a look at the picture below. This is a collection of insects (snails are not insects, but we will not quibble) of different shapes and sizes. And now divide them into several groups according to the degree of similarity. No catch. Start by grouping spiders.
Finished? Although there is no “right” decision here, you must have divided these creatures into four
clusters . In one cluster there are spiders, in the second - a pair of snails, in the third - butterflies, and in the fourth - a trio of bees and wasps.
Well done, right? You could probably do the same if there were twice as many insects in the picture. And if you had plenty of time - or a craving for entomology - then you probably would have grouped hundreds of insects.
However, for a machine, grouping ten objects into meaningful clusters is not an easy task. Thanks to such a complex branch of mathematics as
combinatorics , we know that 10 insects are grouped in 115,975 ways. And if there are 20 insects, the number of clustering options
will exceed 50 trillion .
With a hundred insects, the number of possible solutions will be greater than the
number of elementary particles in a known Universe . How much more? According to my calculations, about
five hundred million billion billion times more . It turns out more than
four million billion google solutions (
what is Google? ). And this is only for hundreds of objects.
Almost all of these combinations will be meaningless. Despite the unimaginable number of solutions, you yourself very quickly found one of the few useful clustering methods.
We, people, take for granted our excellent ability to catalog and understand large amounts of data. It doesn't matter whether it is text, or pictures on the screen, or a sequence of objects — people, in general, effectively understand the data coming from the outside world.
Considering that the key aspect of developing AI and machine learning is that machines can quickly understand large amounts of input data, how to improve work efficiency? In this article we will look at three clustering algorithms, with the help of which machines can quickly comprehend large amounts of data. This list is far from complete - there are other algorithms - but it is already quite possible to begin with it.
For each algorithm, I will describe when it can be used, how it works, and also give an example with step-by-step parsing. I believe that for a true understanding of the algorithm, you need to repeat its work yourself. If you are
really interested , you will understand that it is best to execute algorithms on paper. Act, no one will judge you!
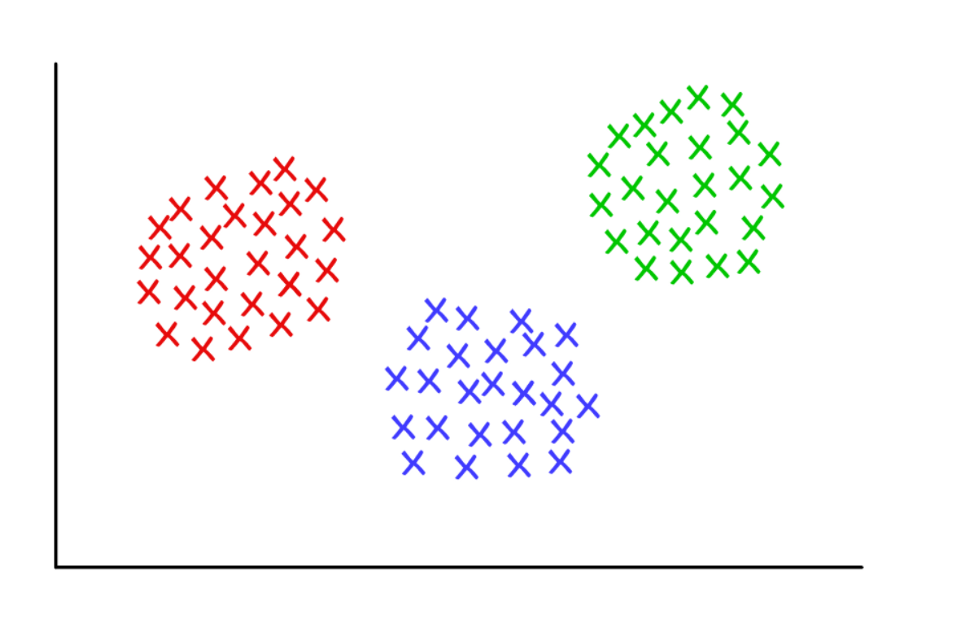Three suspiciously neat clusters with k = 3K-Medium Clustering
Used by:
When you understand how many groups you can get to find
a predetermined (a priori).
How does it work:
The algorithm randomly assigns each observation to one of the
k categories, and then calculates the
average for each category. He then re-assigns each observation to the category with the nearest average, and again calculates the average. The process is repeated until reassignments become unnecessary.
Working example:
Take a group of 12 players and the number of goals scored by each of them in the current season (for example, in the range from 3 to 30). Let's divide the players into, say, three clusters.
Step 1 : you need to randomly divide the players into three groups and calculate the average for each of them.
Group 1 Player A (5 goals), Player B (20 goals), Player C (11 goals) Group Mean = (5 + 20 + 11) / 3 = 12 Group 2 Player D (5 goals), Player E (3 goals), Player F (19 goals) Group Mean = 9 Group 3 Player G (30 goals), Player H (3 goals), Player I (15 goals) Group Mean = 16
Step 2 : reassign each player to the group with the nearest average. For example, player A (5 goals) is sent to group 2 (average = 9). Then again we calculate the averages by groups.
Group 1 (Old Mean = 12) Player C (11 goals) New Mean = 11 Group 2 (Old Mean = 9) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) New Mean = 4 Group 3 (Old Mean = 16) Player G (30 goals), Player I (15 goals), Player B (20 goals), Player F (19 goals) New Mean = 21
Repeat step 2 again and again until the players stop changing groups. In this artificial example, this will happen at the next iteration.
Stop! You formed three clusters from dataset!
Group 1 (Old Mean = 11) Player C (11 goals), Player I (15 goals) Final Mean = 13 Group 2 (Old Mean = 4) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) Final Mean = 4 Group 3 (Old Mean = 21) Player G (30 goals), Player B (20 goals), Player F (19 goals) Final Mean = 23
Clusters must match the players' positions on the field - defenders, central defenders and forwards. K-means work in this example because there is reason to assume that the data will be divided into these three categories.
Thus, based on the statistical variation of performance, the machine can justify the location of players on the field for any team sport. This is useful for sports analytics as well as for any other tasks in which dividing datasets into predefined groups helps to draw appropriate conclusions.
There are several variants of the described algorithm. The initial formation of clusters can be done in different ways. We considered the random classification of players into groups, followed by the calculation of averages. As a result, the initial mean values of the groups are close to each other, which increases the repeatability.
An alternative approach is to form clusters consisting of just one player, and then group the players into the nearest clusters. The resulting clusters are more dependent on the initial stage of formation, and the frequency of occurrence in data sets with high variability decreases. But with this approach, fewer iterations may be required to complete the algorithm, because less time will be spent on the separation of groups.
The obvious disadvantage of k-means clustering is that you need
to assume
in advance how many clusters you will have. There are methods for assessing the compliance of a specific set of clusters. For example, the
intracluster sum of squares (Within-Cluster Sum-of-Squares) is a measure of the variability within each cluster. The “better” the clusters, the lower the total intracluster sum of squares.
Hierarchical clustering
Used by:
When you need to open the relationship between the values (observations).
How does it work:
The distance matrix is calculated, in which the cell value (
i, j ) is the metric of the distance between the
i and
j values. Then the pair of the closest values is taken and the average is calculated. A new distance matrix is created, pair values are combined into one object. Then, the pair of the closest values is taken from this new matrix and a new average value is calculated. The cycle repeats until all values are grouped.
Working example:
Take an extremely simplified dataset with several types of whales and dolphins. I am a biologist, and I can assure you that much more properties are used to build
phylogenetic trees . But for our example, we limit ourselves to the characteristic length of the body in six species of marine mammals. There will be two stages of calculation.
Step 1 : calculate the matrix of distances between all types. We will use the Euclidean metric, which describes how far our data are from each other, like settlements on the map. You can get the difference in the length of the bodies of each pair by reading the value at the intersection of the corresponding column and line.
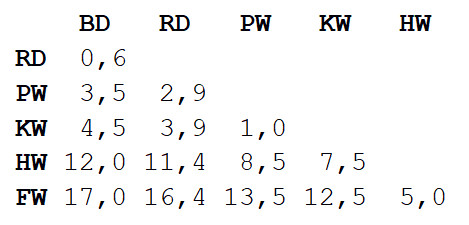Step 2 : Take a pair of two closest species. In this case, it is a bottlenose dolphin and a gray dolphin, in which the average body length is 3.3 m.
We repeat step 1, again calculating the distance matrix, but this time we combine the bottlenose dolphin and the gray dolphin into one object with a body length of 3.3 m.
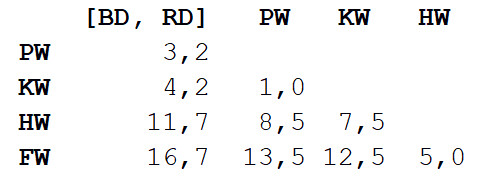
Now repeat step 2, but with a new distance matrix. This time, the closest will be the grind and killer whale, so let's put them together and calculate the average - 7 meters.
Then we repeat step 1: we will again calculate the distance matrix, but with a grind and killer whale as a single object with a body length of 7 m.
Repeat step 2 with this matrix. The shortest distance (3.7 m) will be between the two combined objects, so that we combine them into an even larger object and calculate the average value - 5.2 m.
Then repeat step 1 and calculate the new matrix, combining the bottlenose dolphin / gray dolphin with the grind / killer whale.
Repeat step 2. The shortest distance (5 m) will be between the humpback salmon and the finale, so combine them and calculate the average - 17.5 m.
Again step 1: calculate the matrix.
Finally, we repeat step 2 - only one distance remains (12.3 m), so we will unite everyone into one object and stop. Here's what happened:
[[[BD, RD],[PW, KW]],[HW, FW]]
The object has a hierarchical structure (remember
JSON ), so that it can be displayed in the form of a tree graph or dendrogram. The result is similar to the family tree. The closer two values are on a tree, the more similar or closely related they are.
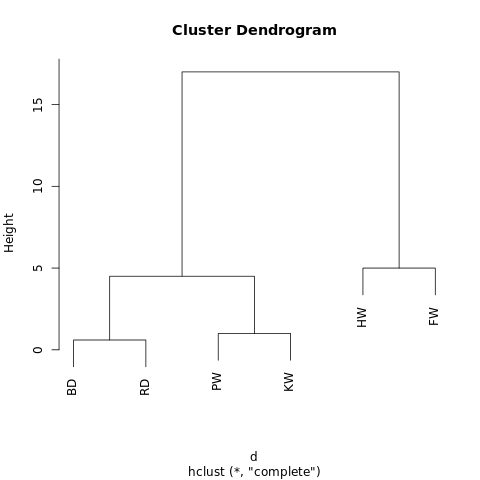Simple dendrogram generated by R-Fiddle.orgThe structure of the dendrogram allows you to understand the structure of the dataset itself. In our example, we have two main branches - one with a humpback whale and a fintail, the other with a bottlenose dolphin / gray dolphin and a grinda / killer whale.
In evolutionary biology, much larger data collections with many species and abundant traits are used to identify taxonomic links. Outside of biology, hierarchical clustering is applied in the areas of Data Mining and machine learning.
This approach does not require to predict the desired number of clusters. You can split the resulting dendrogram into clusters, “cutting” the tree at the desired height. The height can be selected in different ways, depending on the desired resolution of the data clustering.
For example, if the above dendrogram is cut at a height of 10, then we will cross two main branches, thereby dividing the dendrogram into two graphs. If, however, cut at a height of 2, then we divide the dendrogram into three clusters.
Other hierarchical clustering algorithms may differ in three aspects from those described in this article.
The most important thing is the approach. Here we used the
agglomerative (agglomerative) method: we started with separate values and cyclically clustered them until we had one large cluster. An alternative (and computationally more complex) approach implies a reverse sequence: first, one huge cluster is created, and then sequentially divided into smaller and smaller clusters, until individual values remain.
There are also several methods for calculating distance matrices. The Euclidean metric is sufficient for most tasks, but in some situations
other metrics are better suited.
Finally, linkage criterion may vary. The connection between clusters depends on their proximity to each other, but the definition of “proximity” is different. In our example, we measured the distance between the average values (or “centroids”) of each group and combined the nearest groups in pairs. But you can use another definition.
Suppose each cluster consists of several discrete values. The distance between two clusters can be defined as the minimum (or maximum) distance between any of their values, as shown below. For different contexts, it is convenient to use different definitions of the join criterion.
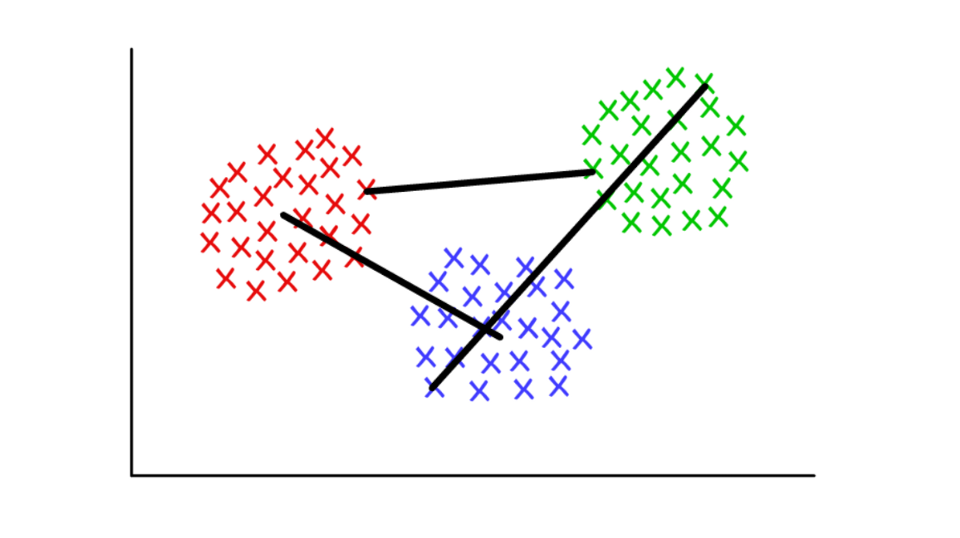Red / blue: centroid union; red / green: minimum based combining; green / blue: max-based pooling.Graph Community Detection
Used by:
When your data can be represented as a network, or "graph".
How does it work:
A community in a graph (community community) can be very roughly defined as a subset of vertices that are more connected with each other than with the rest of the network. There are different community definition algorithms based on more specific definitions, for example, Edge Betweenness, Modularity-Maximsation, Walktrap, Clique Percolation, Leading Eigenvector ...
Working example:
Graph theory is a very interesting section of mathematics that allows us to model complex systems in the form of abstract sets of “points” (vertices, nodes) connected by “lines” (edges).
Perhaps the first application of graphs that comes to mind is the study of social networks. In this case, the vertices represent people who are connected to the edges with friends / subscribers. But you can imagine any system in the form of a network, if you can justify the method of meaningful connection of components. Innovative applications of clustering using graph theory include extracting properties from visual data and analyzing genetic regulatory networks.
As a simple example, let's look at the graph below. Here are eight sites that I visit most often. Links between them are based on links in articles on Wikipedia. Such data can be collected manually, but for large projects it is much faster to write a script in Python. For example:
https://raw.githubusercontent.com/pg0408/Medium-articles/master/graph_maker.py .
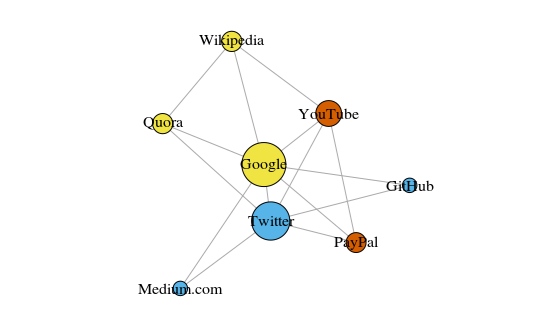The graph is built using the igraph package for R 3.3.3The color of the peaks depends on the participation in the communities, and the size depends on the
centrality (centrality). Please note that the most central are Google and Twitter.
Also, the resulting clusters very accurately reflect real tasks (this is always an important indicator of performance). Yellow highlighted vertices representing reference / search sites; blue highlighted sites for online publications (articles, tweets or code); red highlights PayPal and YouTube, founded by former PayPal employees. A good deduction for the computer!
In addition to visualizing large systems, the real power of networks lies in mathematical analysis. Let's start with the transformation of pictures of the network in a mathematical format. Below is the
adjacency matrix of the network.
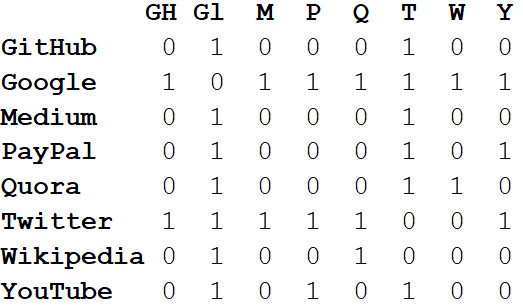
The values at the intersections of the columns and rows indicate whether there is an edge between this pair of vertices. For example, it exists between Medium and Twitter, so it is 1. At the intersection of this line and column, there is no edge between Medium and PayPal, so there is 0 in the corresponding cell.
If we present all the properties of the network in the form of an adjacency matrix, this will allow us to draw all sorts of useful conclusions. For example, the sum of the values in any column or row characterizes the
degree of each vertex — that is, the number of objects connected to that vertex. Usually denoted by the letter
k .
If we sum up the degrees of all the vertices and divide by two, then we get L - the number of edges in the network. And the number of rows and columns is N - the number of vertices in the network.
Knowing only k, L, N and the values in all the cells of the adjacency matrix A, we can calculate the modularity of any clustering.
Suppose we cluster a network for a certain number of communities. Then you can use the value of modularity to predict the "quality" of clustering. Higher modularity suggests that we have divided the network into “exact” communities, and lower modularity suggests that clusters are formed by chance rather than reasonably. To make it clearer:
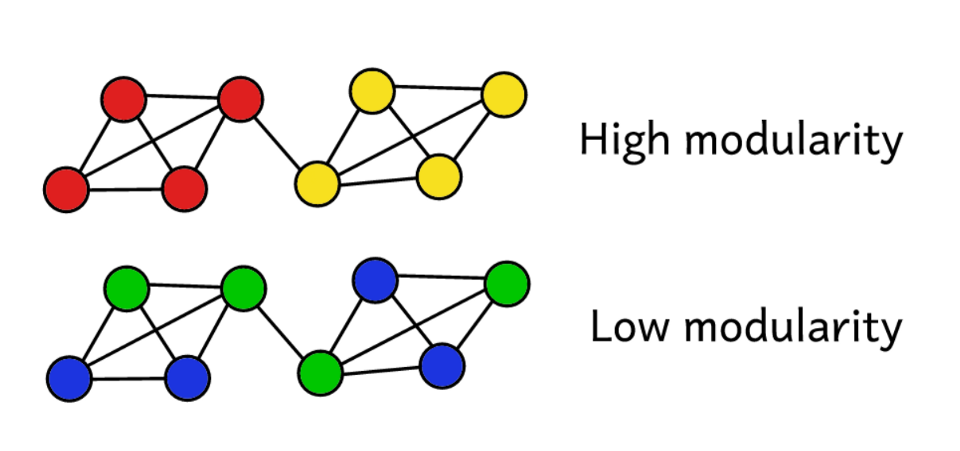
Modularity is a measure of the "quality" of groups.
Modularity can be calculated using the following formula:
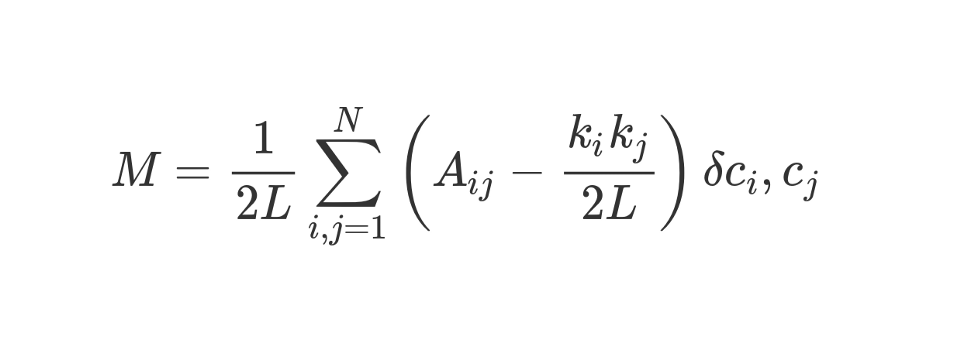
Let's take this rather frightening looking formula.
M , as you understand, this is modularity.
The coefficient
1 / 2L means that we divide the rest of the “body” of the formula by 2L, that is, by double the number of edges in the network. In Python, you could write:
sum = 0 for i in range(1,N): for j in range(1,N): ans =
What is
#stuff with i and j ? The bit in parentheses tells us to subtract (k_i k_j) / 2L from A_ij, where A_ij is the value in the matrix at the intersection of row i and column j.
The values of k_i and k_j are the degrees of each vertex. They can be found by summing the values in row i and column j, respectively. If we multiply them and divide by 2L, then we will get the expected number of edges between vertices i and j, if the network were randomly mixed.
The contents of the brackets reflect the difference between the actual structure of the network and the expected one if the network were re-arranged randomly. If you play with the values, then the highest modularity will be at A_ij = 1 and low (k_i k_j) / 2L. That is, modularity increases if there is an “unexpected” edge between vertices i and j.
Finally, multiply the contents of the brackets by what is designated in the formula as δc_i, c_j. This is the Kronecker-delta symbol. Here is its implementation in Python:
def Kronecker_Delta(ci, cj): if ci == cj: return 1 else: return 0 Kronecker_Delta("A","A")
Yes, so simple. The function takes two arguments, and if they are identical, it returns 1, and if not, then 0.
In other words, if the vertices i and j fall into one cluster, then δc_i, c_j = 1. And if they are in different clusters, the function returns 0.
Since we multiply the contents of the brackets by the Kronecker symbol, the result of the nested sum
Σ will be the highest when the vertices inside one cluster are joined by a large number of “unexpected” edges. Thus, modularity is an indicator of how well a graph is clustered into individual communities.
The division by 2L limits the unit to the upper modularity. If the modularity is close to 0 or negative, it means that the current clustering of the network does not make sense. By increasing modularity, we can find the best way to cluster the network.
Please note that to assess the "quality" of cluster clustering, we need to determine in advance how it will be clustered. Unfortunately, unless the sample is very small, because of computational complexity, it is simply physically impossible to stupidly go through all the methods of graph clustering, comparing their modularity.
Combinatorics suggests that for a network with 8 vertices, there are 4140 clustering methods. For a network with 16 vertices, there will already be more than 10 billion ways, for a network with 32 vertices, 128 septillons, and for a network with 80 vertices, the number of clustering methods will exceed the
number of atoms in the observed Universe .
Therefore, instead of brute force, we use the heuristic method, which will make it relatively easy to calculate clusters with maximum modularity. This is an algorithm called
Fast-Greedy Modularity-Maximization , a kind of analogue of the agglomerative hierarchical clustering algorithm described above. Instead of combining on the basis of proximity, Mod-Max unites communities depending on modular changes. How it works:
First, each vertex is assigned to its own community and the modularity of the entire network is calculated - M.
Step 1 : for each pair of communities connected by at least one edge, the algorithm calculates the resulting change in modularity ΔM in the case of the union of these pairs of communities.
Step 2 : then the pair is taken, when combined, the ΔM will be maximum, and combined. For this clustering, a new modularity is computed and saved.
Steps 1 and 2 are
repeated : each time a pair of communities is combined, which gives the greatest ΔM, a new clustering scheme and its M. are preserved.
Iterations
stop when all vertices are grouped into one huge cluster. The algorithm now checks the stored records and finds the clustering scheme with the highest modularity. This is what comes back as a community structure.
It was computationally difficult, at least for people. Graph theory is a rich source of difficult computational problems and NP-hard problems. With the help of graphs, we can draw many useful conclusions about complex systems and datasets. Ask Larry Page, whose PageRank algorithm — which helped Google transform from a startup into a global dominant in less than a single generation — is entirely based on graph theory.
In studies devoted to graph theory, the focus today is on the definition of communities. There are many alternatives to the Modularity-Maximization algorithm, which, although useful, is not without flaws.
First, with an agglomerative approach, small, well-defined communities are often combined into larger ones. This is called the resolution limit - the algorithm does not allocate communities smaller than a certain size. Another disadvantage is that instead of a single pronounced, easily achievable global peak, the Mod-Max algorithm tends to generate a broad “plateau” of many close modularities. As a result, it is difficult to select a winner.
Other algorithms use different ways to define communities. For example, Edge-Betweenness is a divisional (separation) algorithm that starts by grouping all the vertices into one huge cluster. Then the least “important” edges are iteratively removed until all the vertices are isolated. It turns out a hierarchical structure in which the vertices are closer to each other, the more they are similar.
The algorithm, Clique Percolation, takes into account possible intersections between communities. There is a group of algorithms based on a
random walk on a graph, and there are methods of
spectral clustering , which deal with spectral decomposition (eigendecomposition) of the adjacency matrix and other matrix derivatives derived from it. All these ideas are used to highlight the signs, for example, in computer vision.
We will not analyze working examples for each algorithm in detail. , , 20 .
Conclusion
, - , , . , , 20-40 .
, — , . , , .
, , , , . , - , , ? - !